数学建模（二）

2022美赛备战

2022年数学建模美赛备战参考——数学建模清风_哔哩哔哩_bilibili

题目分析

MCM（数学建模竞赛）：A,B,C
ICM（交叉学科竞赛）：D,E,F

MCM要求更深的数学功底和变成基础
ICM要求写作和逻辑能力

A：连续型
B：离散型
C：数据挖掘
D：运筹学和网络科学
E：环境科学
F：政策相关的题目

EF

E,F是最简单的题目，题目要求我们自己收集数据，用到的模型：评价类模型，相关性分析，回归分析，拟合；
E,F比较开放，题目中的小问比较多，因此需要重视写作，论文的结构要求清晰
美赛不需要提交数据和代码

- 世界数据查找网站：https://www.gapminder.org/data/
- 国家数据查找：到每个国家的统计局官网
- 美赛的题目会给参考文献，可以使用参考文献的数据
- 实在找不到数据：根据实际和逻辑，自己编

D

D题题目固定，涉及到图论，网络分析，优化问题
2020,2021:网络科学
matlab:centrality函数
python:networkx
网络结构可视化软件：gephi——https://gephi.org/
运筹学：排队论，图论，选址优化

C

数据挖掘类题目，根据提供的数据分析出结论
回归分析，时间序列分析，传统机器学习模型
近年来出现了深度学习：2020自然语言处理，2021图像分类
深度学习：B站李沐——https://space.bilibili.com/1567748478
机器学习：https://www.bilibili.com/video/BV1v64y1B7vJ

A B

A——连续
问题中的变量因素是连续变化的，如温度，时间等
B——离散
问题中的变量因素是离散变化的，如数量
连续：微分方程
离散：差分方程

A和B可能会出现一道物理题目，涉及到热力学，流体力学，信号处理
B题目：可能是离散型优化问题，即组合优化问题——智能算法：遗传算法，模拟退火算法

A,B,D可能会用到元胞自动机模型（多主体建模），使用Netlogo仿真模拟软件

常用模型和算法

数学建模竞赛常考三大模型及十大算法_哔哩哔哩_bilibili

三大模型

预测模型（中等难度）

神经网络预测、灰色预测、拟合插值预测（线性回归）、时间序列预测、马尔科夫链预测、微分方程预测、Logistic 模型等等。
应用领域：人口预测、水资源污染增长预测、病毒蔓延预测、竞赛获胜概率预测、月收入预测、销量预测、经济发展情况预测等在工业、农业、商业等经济领域，以及环境、社会和军事等领域中都有广泛的应用。

优化模型（偏难）

规划模型（目标规划、线性规划、非线性规划、整数规划、动态规划）、图论模型、排队论模型、神经网络模型、现代优化算法（遗传算法、模拟退火算法、蚁群算法、禁忌搜索算法）等等。
应用领域：快递员派送快递的最短路径问题、水资源调度优化问题、高速路口收费站问题、军事行动避空侦察的时机和路线选择、物流选址问题、商区布局规划等各个领域。

评价模型（偏简单）

模糊综合评价法、层次分析法、聚类分析法、主成分分析评价法、灰色综合评价法、人工神经网络评价法等等。
应用领域：某区域水资源评价、水利工程项目风险评价、城市发展程度评价、足球教练评价、篮球队评价、水生态评价、大坝安全评价、边坡稳定性评价

十大算法

蒙特卡洛算法
又称为随精选模拟算法，
是通过计算机仿真来解决问题的算法，同时可以通过模拟来检验自己模型的正确性，是比赛时，必用的方法
数据处理算法
数据拟合，参数估计，插值等：
比赛在通常会遇到大量的数据需要处理，而处理数据的关键就在于这些算法，通常使用matlab作为工具
规划类问题算法
线性规划，整体规划，多元规划，二次规划等规划类问题：
建模比赛中大数问题属于最优化问题，很多时候这些问题可以用数学规划算法来解决，通常使用Lindo，Lingo等软件实现
图论算法
最短路径，网络流，二分图等算法
动态规划，回溯搜索，分治算法，分支定界
最优化理论三大经典算法
模拟退火算法，遗传算法，神经网络
网格算法，穷举法
连续离散化方法
数值分析算法
图像处理算法

美赛论文写作

数学建模清风——论文写作方法教程（国赛和美赛）_哔哩哔哩_bilibili
MCM: The Mathematical Contest in Modeling (comap.com)

2022 Contest Dates and Times:

Registration Deadline: Before 3:00 p.m. EST on Thursday, February 17, 2022.
Contest Starts: 5:00 p.m. EST on Thursday, February 17, 2022.
Contest Ends: 8:00 p.m. EST on Monday, February 21, 2022.
Solution Report Deadline: 9:00 p.m. EST on Monday, February 21, 2022.
Contest Results: The results will be posted on or before May 20, 2022.

2022美赛的关键时间节点报名截止时间美国东部时间2022年2月17日 15:00之前（星期四）北京时间2022年2月18日凌晨4:00之前（星期五）
比赛开始时间美国东部时间2022年2月17日 17:00（星期四）北京时间2022年2月18日上午6:00（星期五）
比赛截止时间美国东部时间2022年2月21日 20:00（星期一）北京时间2022年2月22日上午9:00（星期二）
提交方案截止时间美国东部时间2022年2月21日 21:00（星期一）北京时间2022年2月22日上午10:00（星期二）
比赛结果公布时间美国东部时间2022年5月20日之前发布

Summary Sheet 摘要页（超级重要）

布局

开头段（必要）
- 3-5行，2-3句话 
针对问题1
针对问题2
针对问题3
结尾段（可选）

开头段（必要）
- 3-5行，2-3句话 
Firstly
Then
Next
Finally
结尾段（可选）

不能超过一页，读者在不阅读全文的情况下，就能获得必要的信息

摘要包含的三要素：解决了什么问题，应用了什么方法，得到了什么结果

概括全文，行文简洁，突出论文的新见解，新方法和特色，不能有主观性

摘要是其他部分都写完之后，再来书写（半天时间）

摘要的开头段

三句话，三到五行

第一句话简单交代题目的背景（可选）

第二句话交代你们所作的事情（最重要）

第三句话说以先解决这个问题的实际意义（少部分论文有）

摘要的中间段

解决了什么问题，应用了什么方法，得到了什么结果

解决了什么问题：不单独提出我们要解决的问题，因为后面的两个要素会提到
应用了什么方法：紧扣题目
得到了什么结果：

摘要的结尾段

介绍论文的亮点，对类似问题进行适当的推广

如果不会写的话，可以不写结尾段

不要出现的废话
论文的标题title和关键词key world

标题和关键词要求不严格

Contents 目录

目录快速生成——排版课程

正文1 Introduction 引言

引言包含了两到三个小部分

Problem Background 问题背景

总结题目所给的背景

结合自己对赛题的理解，讲背景介绍有侧重的往自己研究的方向去靠

Restatement of the Problem 问题重述

1和2可以合并为一点
Literature Review 文献综述

这部分主要是总结以前的学者针对这个问题已经做的研究。事实上，绝大多数期刊发表的论文都会有文献综述部分。但在美赛特等奖论文中，只有不到30%的论文有这一部分，不是说这部分不重要，而是这一部分很难写。

注意：文献综述本身就是一种文体，可以作为论文独立发表，也可以放在论文中作为独立的一个部分；我们在美赛中写的文献综述不需要达到上面定义写的
这么严格的标准。

总结写作特点：有很多学者都研究过这个问题(红色圈出来的编号就是参考文献的标记)，其中：

某某学者建立了某某模型或者使用了某某方法研究了这个问题；

某某学者通过研究了这个问题得到了某某结论。

技巧：文献综述中的文章能直接和你的论文中使用的模型或者得到的结论相互呼应！

Our work 我们的工作

大家如果看特等奖论文的话，会发现很多论文在这一部分都绘制了一个漂亮的图形来介绍文章的思路，大
家可以模仿模仿。

正文2 Assumptions and Justifications 模型假设

美赛要求较高

正文3 Notations 符号说明

Glossary——术语汇编

正文4 5 6 模型的建立与求解(正文最重要的部分)

模型建立：模型建立是将原问题抽象成用数学语言的表达式，它一定是在先前的问题分析和模型假设的基础上得来的。因为比赛时间很紧，大多时候我们都是使用别人已经建立好的模型。这部分一定要将题目问的问题和模型紧密结合起来，切忌随意套用模型。我们还可以对已有模型的某一方面进行改进或者优化，或者建立不同的模型解决同一个问题，这样就是论文的创新和亮点。

模型求解：把实际问题归结为一定的数学模型后，就要利用数学模型求解所提出的实际问题了。一般需要借助计算机软件进行求解，例如常用的软件有Matlab, Spss, Lingo, Excel, Stata, Python等。求解完成后，得到的求解结果应该规范准确并且醒目，若求解结果过长，最好编入附录里。（注意：如果使用智能优化算法或者数值计算方法求解的话，需要简要阐明算法的计算步骤）

每个模型作为一个单独的大标题

而美赛的命名方式五花八门，有些论文使用建立的模型的名称命名；有些使用论文要解决的问题命名；也有些论文使用和国赛一样简单粗暴的方
式命名。

可以以要解决的问题命名也可以以求解问题命名

明确题意后，简述基本思路。首先，简要介绍利用的基本原理和基本思想，再进行构建基本模型，如数学表达式、算法流程图等，要明确说明解题的思想和思路，有逻辑性、合理性、可行性，需要完整叙述。也可以结合实际问题，进行改进和完善基本模型，使其能有效、实用解决问题。

三点要求：

必须要有数学模型：即数学公式组成的一套数学结构、或者是一套数学的解决方案等；

模型要求表达完整，正确和简明；

模型要有实用性，要能求解出来，以能够解决问题为原则。

模型求解的注意事项：

1）国赛中常出优化类问题，如果你用到了启发式算法求解的话，一定要简要写明算法步骤，并要结合具体的问题来阐明计算的思路。

2）求解的结果应该在论文中突出的展示出来，有具体答案的问题比较简单，直接放上数值计算结果即可；如果是开放类问题的话，一定要对结果进行阐明
和解释，如果能加上美观整洁的图表就更好了。

正文 Data Description 数据描述(不常见)

Data Description翻译过来就是数据描述。注意，这部分内容不是必须的，大家根据自己的需要来进行添加。
如果自己收集了数据或者题目给了数据的话，可以先对数据进行一个简单的介绍，或者将数据可视化，然后再从图形中得到一些直观的结论。
这里给大家一些相关的术语的翻译：

• Data Collection(数据的收集)

• Data Pre-processing(数据预处理) / Data Cleaning(数据清洗)

• Data Visualization(数据可视化)

• Descriptive Statistical Analysis of the Data(数据的描述性统计分析)

这部分内容在论文中的位置也比较灵活，我们可以将这个内容放到模型的建立与求解中，也有部分论文放在了引言部分，还有的论文将这个内容放到“Model Preparation模型准备”这个部分，这种见得比较少，我们之前在国赛论文框架中介绍过模型准备的写法。特别的，如果做的是美赛C题（C题一般是数据分析类型的题目），我们可以把这个部分单独作为一个大的部分，然后进行数据预处理和数据可视化分析。

正文7 Sensitivity Analysis 灵敏度分析（重要）(不是很懂)

数学建模中的灵敏度分析，到底在分析什么？ - 知乎 (zhihu.com)

在这个部分中，我介绍了灵敏度分析、误差分析和稳定性检验的写法，其中稳定性检验和灵敏度分析非常类似，因此大家要掌握的就是前面两种分析的写法。

在美赛的写作中，写的最多的就是灵敏度分析，因此这里我们的标题就直接取得是Sensitivity Analysis; 如果你既要写灵敏度分析，又要写误差分析，那么你可以把标题改成： Sensitivity Analysis and Error Analysis. 注意： • 误差分析一般翻译为：Error Analysis • 稳定性检验的别称较多，还可以称为稳健型检验或稳健型分析，因此它的翻译也较多，可翻译为：Stability Test、 Robustness Test或者Robustness Analysis

模型的分析：在建模比赛中模型分析主要有两种，一个是灵敏度(性)分析，另一个是误差分析。灵敏度分析是研究与分析一个系统（或模型）的状态或输出变化对系统参数或周围条件变化的敏感程度的方法。其通用的步骤是：控制其他参数不变的情况下，改变模型中某个重要参数的值，然后观察模型的结果的变化情况。误差分析是指分析模型中的误差来源，或者估算模型中存在的误差，一般用于预测问题或者数值计算类问题。

模型的检验：模型检验可以分为两种，一种是使用模型之前应该进行的检验，例如层次分析法中一致性检验，灰色预测中的准指数规律的检验，这部分内容应该放在模型的建立部分；另一种是使用了模型后对模型的结果进行检验，数模中最常见的是稳定性检验(有的论文也称为稳健型检验或稳健型分析)，实际上这里的稳定性检验和前面的灵敏度分析非常类似，等会大家看到例子就明白了。

正文8 Model Evaluation and Further Discussion 模型的评价和进一步的讨论

该部分可以翻译为模型的评价和进一步的讨论，对应于国赛框架中的模型的评价、改进与推广部分

我们可以把这个大的部分拆分成三个小部分写：

（1）Strengths 这里写论文或者模型的优点
（2）Weaknesses 这里写缺点：缺点写的个数一般要比优点少
（3） Further Discussion 进行进一步的讨论，这里可以写模型的改进和拓展。
模型改进：Model Improvements 模型拓展：Model Extensions
（这里单词写的都是复数形式，如果你只写了一点就改成单数形式）
另外，本部分的标题需要根据你的内容进行调整，例如：如果你没有写进一步讨论的话，就直接把标题写成模型的评价Model Evaluation 。

正文9 Conclusion 结论

Conclusion翻译过来就是结论，这个部分在国赛论文几乎见不到，但在美赛中出现的频率很高。

这个部分可以是论文中心思想的重申、研究结果或主要观点的归纳，也可以是某些启示性的解释或考虑。

有些论文把“Model Evaluation and Further Discussion”的内容放到了结论部分.

注意区分这三个部分！！！！！！

References 参考文献

本部分是参考文献，在美赛中，参考文献不要出现中文！如果要引用中文论文或者书籍怎么办？请自己翻译

Appendices 附录

附录中的代码也不要出现中文注释，也就是任何地方都不要出现中文

Article 杂志文章

美赛有些题目会要求大家给某个杂志写一篇文章(Article)

（1）2020A题 In addition to your technical report, prepare a one- to two-page article for Hook
Line and Sinker magazine to help fishermen understand the seriousness of the problem and how your proposed solution(s) will improve their future business prospects.

除了你的技术报告，准备一到两页的文章，作为Hook Line and Sinker 的杂志内容，以帮助渔民了解问题的严重性，以及你的解决方案将如何改善他们未来的业务前景。
（2）2020B题 Finally, write an informative, one- to two-page article describing your model and
its results for publication in the vacation magazine: Fun in the Sun, whose readers are mainly non-technical.
最后，写一篇内容丰富的一到两页的文章，描述你的模型及其结果，发表
在假期杂志上：Fun in the Sun ，读者都是小白，不懂太复杂的模型。

文章中不要写太过专业的话，确保你的读者能读得懂！

Letter 写信

Memo 备忘录

美赛论文排版

数学建模清风——论文排版教程_哔哩哔哩_bilibili

LaTex学习成本太大了，因此使用Word进行排版。

优秀论文共同特点：

（1）整体结构完整，大多数论文都是使用三级标题式进行布局；

（2）论文正文部分排版紧凑，没有大段空行，内容看上去翔实；

（3）表格整洁，一般使用三线表形式，表格上方有对应的标题；

（4）图形清晰美观，下方有对应的标题，文中要解释图形意义；（表上图下）

（5）公式编辑规范，大部分论文使用公式编辑器，且带有编号。

Word 基础知识

F4键的作用是重复上一步操作，在PPT和Excel中也是同样的作用。

首行缩进不要打两个空格，应该在开始-段落中设置首行缩进

Ctrl+Enter：分页符

Delete：大多数时候我们删除某个内容使用的都是退格键，但有时候排版的时候，你会发现使用退格键删除后论文的排版格式乱掉了（特别是有表格需要排版的时候用的很多），这时候可以考虑使用删除键。我们以后遇到了再来给大家强调这一点。

格式刷：先复制需要的格式，然后点击格式刷，点击格式刷一次，只能进行一次格复制，点击两次能进行无数次格式复制

左对齐，居中对齐，右对齐，两端对齐，分散对齐

项目符号，编号，多级列表

样式和多级列表

论文模板

（1）论文的首页是摘要页，论文标题使用三号黑体，摘要两个字使用四号黑体， 关键词两个字使用小四黑体。 
（2）论文的正文部分使用小四宋体(中文)和小四Times New Roman字体(西文)， 行距设置为单倍，首行缩进两个字符。 
（3）一级标题使用四号黑体，无缩进居中对齐，段前段后6磅，单倍行距，编号 使用“一、二、三、四、”等。
（4）二级标题使用小四黑体，无缩进左对齐，段后6磅，单倍行距，编号使用 “1.1 1.2 2.1 2.2 2.3 ”等。 
（5）三级标题使用小四黑体，无缩进左对齐，单倍行距，编号使用“3.1.1 3.1.2 5.3.1 5.3.2 ”等。不建议使用三级以上的标题，看起来太长了。 
（6）论文中的图片、表格居中对齐，无缩进；表格上方和图片下方的标题使用五号宋体加粗(中文)和五号Times New Roman字体加粗(西文)，无缩进，居中对齐。

表格的制作和排版

三线表

使用边框刷子：点顶线：1.5磅；栏目线：0.75磅；底线：1.5磅

文字：水平居中

分布行，分布列：把表格的行和列都变成一样大小

制作三线表的模板

长表格的处理：excel预处理

宽表格的处理：excel预处理

两个并排的独立表格：excel预处理

有合并单元格的表格：先用excel预处理，断点用白色的边框替代

Stata的回归结果表格：

SPSS输出的表格：

文章或报告的封面：

自动生成表的标题：选中表格-引用-插入题注

文章的内容与表格相关联，如：结果请见表2，引用-交叉引用

Ctrl+A，全选，然后按F9，可以刷新整篇文章

文字与表格或者图像之间的间距可以设置为0.5行

图形的制作和排版

国赛中的图要求简约

美赛中的图要求美观，吸人眼球

图片首先设置无缩进，然后居中对齐，再在图片下边写上编号和图片的标题

（记住：表上图下，即表的标题在上面，图的标题在下面）

图片的制作

matlab或者python
excel，spss，origin
展示模型或者算法过程的流程图
描述问题分析或者建模思路的示意图

使用PPT绘制思维导图——SmartArt

Xmind

绘制示意图——PPT，Draw.io

绘制带用矢量图的示意图——阿里巴巴矢量图库，Islide矢量图插件，Draw.io

对图像的加工——PPT等

流程图的绘制：Draw.io

物理示意图的绘制：PPT，AxGraph(有水印)

应用下载 – GeoGebra

Apache ECharts

商业智能和分析软件 (tableau.com)

数据可视化 | Microsoft Power BI

社会网络图

手动：Gelphi，yEd - Graph Editor (yworks.com)
python的nerworkx包

地理数据可视化GIS——经纬度可视化

专业：ArcGIS，MapGIS，supermap
Tableau，Power BI
python的folium包

使用Excel地图数据可视化——中国和美国的地图都有了

对任意国家的地图进行可视化设计：Pixel Map Generator | amCharts（中国地图有问题）

图例，用PPT中的表格

中国以及各个省市的地图：[阿里云 DataV - 数据可视化平台 (aliyun.com)](http://datav.aliyun.com/portal/school/atlas/area_selector)

公式的编辑和排版

LaTex：在线LaTeX公式编辑器-编辑器 (latexlive.com)

【老湿基】为妈咪叔 LaTeXLive.com 网页程序打call｜侠之大者，为国为民！_哔哩哔哩_bilibili

Word自带的公式编辑器：alt和=同时按下

AxMath：免费部分功能

MathTpye：收费

将公式识别为LaTex代码：Mathpix Snip，Mathpix每个月能免费用50次

在线LaTeX公式编辑器-编辑器 (latexlive.com)：也可以进行公式的识别

AxMath：

公式的自动编号

行内公式

行间公式——编号

插入公式时候出现的问题

公式上浮问题

选中段落，右键-段落-中文版式-将文本对齐方式改为居中-确定

公式的间距过大——行内公式

选中段落，右键-段落-取消勾选下面的这两个框

公式编辑器中不要出现中文

参考文献的排版

要求：所有引用他人或公开资料(包括网上资料)的成果必须按科技论文的规范列出参考文献，并在正文引用处予以标注(引用-交叉引用)。

我这里教给大家三种方案： 
（1）自己手动设置参考文献（数模论文的参考文献不是很多，而且要求也没有那 么严格，因此推荐大家在数学建模比赛的论文中使用，这样比较节省时间） 
（2）使用专业的文献管理软件，例如EndNote（需要下载软件并学习额外的操作， 如果你以后不走学术路线的话，可能使用的机会不是很多）
（3）Word自带的插入引文功能（插入引文的操作比较繁琐，不推荐大家使用）

附录的排版

代码高亮：代码在线高亮工具 | 将高亮美化的代码一键粘贴到 Word 或 OneNote 中 (highlightcode.com)

代码在线高亮 | 菜鸟工具 (runoob.com)

在线代码着色高亮 (oschina.net)

CodeInWord|在word中优雅展现的代码|代码高亮|word中插入代码|代码格式化

Ubuntu Pastebin——支持Matlab

美赛论文排版要求

目录过长，目录页超过了一页，可以把显示级别设置为2

用表格设置并排的图片

表格的嵌套

英文段字效果

机器学习

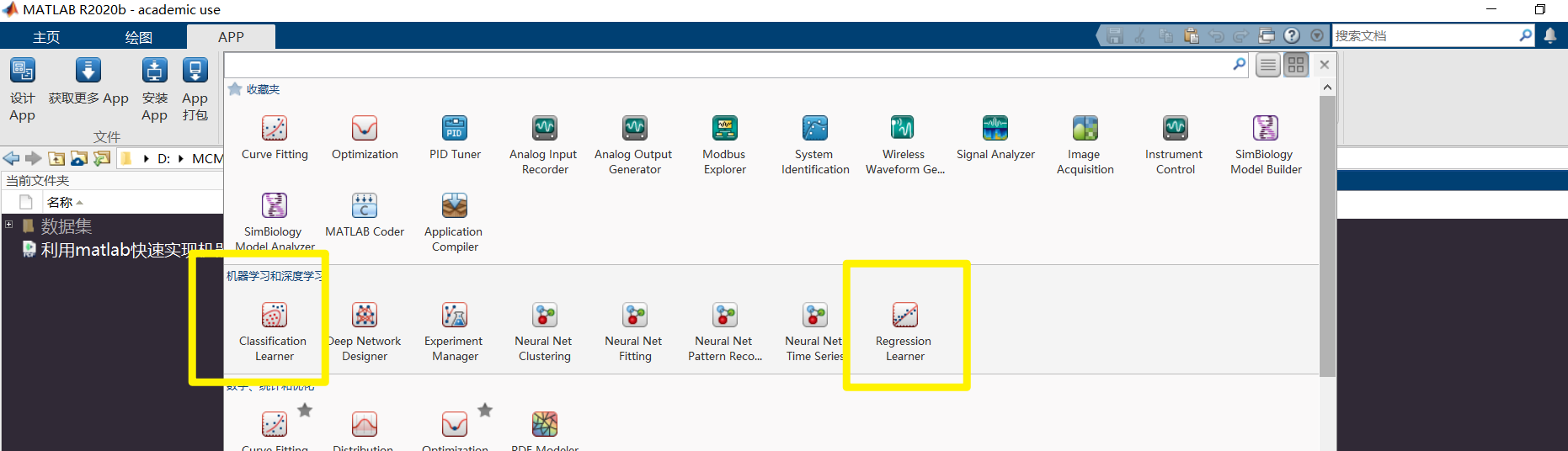
数学建模清风第四次直播：利用matlab快速实现机器学习_哔哩哔哩_bilibili

资料——提取码：kkkk

基本概念和分类

机器学习：

书中对于机器学习的一个定义：

机器学习正是这样一门学科,它致力于研究如何通过计算的手段,利用经验来改善系统自身的性能.在计算机系统中，“经验”通常以 “数据”形式存在,

因此,机器学习所研究的主要内容,是关于在计算机上从数据中产生“模型”(model)的算法，即“学习算法”(learning algorithm).

有了学习算法,我们把经验数据提供给它,它就能基于这些数据产生模型;在面对新的情况时(例如看到一个没剖开的西瓜),模型会给我们提供相应的判断(例如好瓜)．

机器学习：监督学习（supervised learning），无监督学习(unsupervised learning)，强化学习(reinforcement learning)，半监督学习(semi-supervised learning)，主动学习(active learning)

监督学习

监督学习是指从标注数据中学习预测模型的机器学习问题。标注数据表示输入输出的对应关系，预测模型对给定的输入产生响应的输出。监督学习的本质是学习输入到输出的映射统计规律。

翻译成白话：我们的数据既有输入变量又有输出变量（既有特征 feature 又有标签 label），我们要找到输入变量和输出变量之间的关系。

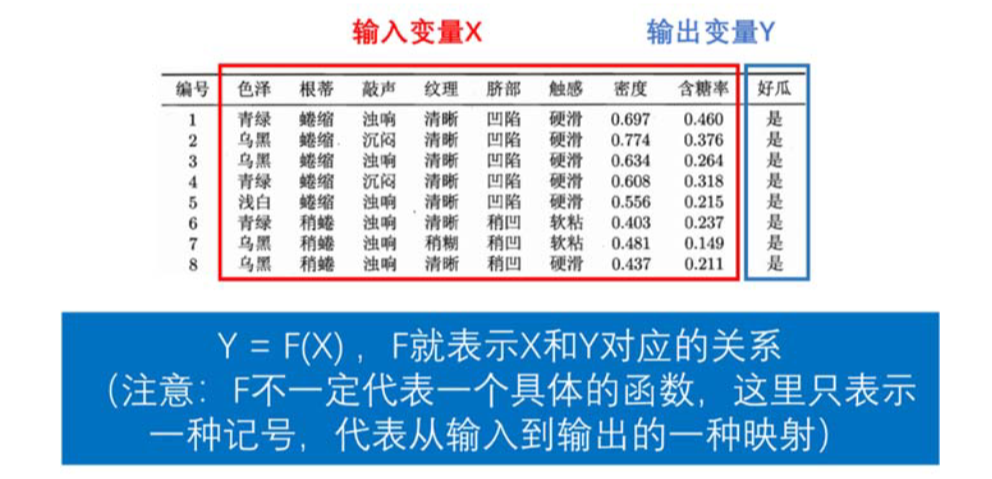
监督学习根据输出变量Y的数据类型不同，又可以分成两种类型：

（1）当输出变量Y取有限个离散值时，称为分类问题。

举例：

 判断西瓜的好坏（好瓜/坏瓜）

 判断肿瘤的性质（良性/恶性）

 根据鸢尾花的花萼长度、花萼宽度、花瓣长度和花瓣宽度这四个指标来判断它的种类（山鸢尾/杂色鸢尾/维吉尼亚鸢尾）

在分类问题中，当Y只取两类时，我们称为二分类问题，

当分类的类别为多个时，称为多分类问题。

（2） 输出变量Y为连续型变量，称为回归问题。（此回归非彼回归）

举例：

 给定房屋的一些信息（户型、是否靠近地铁等），预测房价
 给定土地的施肥量，预测农作物的产量

无监督学习

无监督学习是指从无标注数据中学习预测模型的机器学习问题。无标注数据是自然得到的数据，预测模型表示数据的类别、转换或概率。无监督学习的本质是学习数据中的统计规律或潜在结构。

翻译成白话：我们的数据全部都是输入变量，没有输出变量。我们希望得到数据之间隐藏着的结构和规律。

无监督学习最常见的两种用法：聚类和降维。

聚类的例子：银行收集了客户的许多个人信息，根据这些个人信息可以将客户划分到不同的用户群体（例如：贵宾客户、重点客户、普通客户、可能流失的客户等），银行可以为不同的用户群体制定出相应的个性化营销方案。

降维的例子：输入变量的维度太大（指标个数太多了），我们需要通过降维的方法来构造出少数几个指标，这几个指标能保留原来这些输入变量的绝大部分信息。

注意：有很多同学区分不开聚类和分类的概念，事实上你只要知道监督学习和无监督学习的核心区别就行了（有无输出变量Y）。

在分类中，类别是已知的；而在聚类中，类别是不知道的，我们是通过数据的特征属性将数据划分到某几类中，这几个类代表的含义需要我们自己根据聚类的结果来定义。

半监督学习

数据有：输入变量X和部分输入变量的输出Y

强化学习

书中的定义：强化学习(reinforcement learning）是指智能系统在与环境的连续互动中学习最优行为策略的机器学习问题。假设智能系统与环境的互动基于马尔可夫决策过程（Markov decision process)，智能系统能观测到的是与环境互动得到的数据序列。强化学习的本质是学习最优的序贯决策。

举个例子：如何让电脑玩游戏？以 flappy bird 这款游戏为例，电脑怎么知道下一步小鸟要采取怎样的行动呢？通过不断与环境的交互和试错的过程，最终完成特定目的或使得整体行动收益最大化。（做对了给奖励，做错了给惩罚）

模型评估的指标（监督学习）

回归问题的评估指标

分类问题的评估指标

混淆矩阵——可以使用matlab自动生成

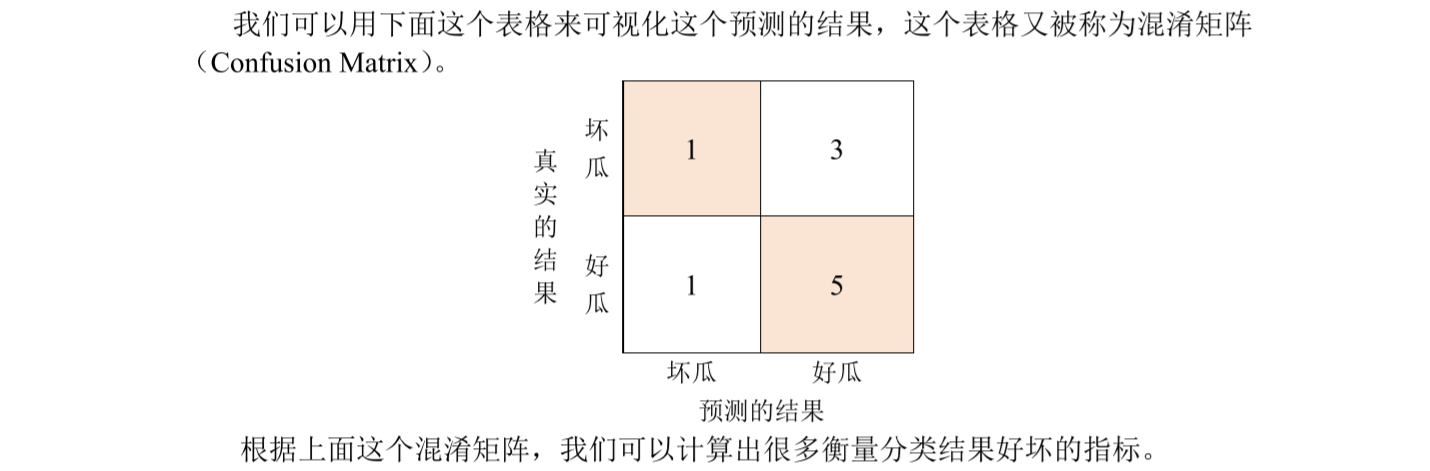
在此之前，我们需要定义分类结果中的正类（positive）和负类（negative），这里的正类和负类实际上借用了医学中的阳性（positive）和阴性（negative）的概念，医学中一般阴性代表正常，而阳性则代表患有疾病。

在机器学习中，我们通常将更关注的事件定义为正类事件。（生活中我们通常会更关注那些结果不好的情况的出现）

例如上面的西瓜分类的例子中，如果我们更关注坏瓜，就定义坏瓜为正类，好瓜为负类。（有些地方也用 0 和 1 表示分类结果，一般正类记为 1，负类记为 0）。

这种划分正类和负类的标准也不是绝对的，如果你更关注好瓜，那么你也可以把好瓜定义成正类；另外有时候我们很难去区分结果的好坏，例如我们要对猫和狗的图片进行分类，这时候正类和负类无论怎么定义都行。

分类准确率，如果样本不平衡，计算出的结果回存在问题，因此这个指标本身存在问题

后两个指标，R和P更重要

通常来说，查全率和查准率是负相关关系的。

怎么理解查全率和查准率的关系：（知乎：李韶华的回答）

假设我们的目的是要找到人群中隐藏的坏人（把坏人当成正类）。如果看重查全率R: 宁可错杀一千个好人，不可漏过一个坏人。（全部识别成坏人
时查全率为1）

如果看重查准率 P: 宁可漏过坏人，不可错杀无辜的好人。（让 FP 尽量小一点，没有充足的证据不会轻易判断一个人是坏人）

查全率和查准率的调和平均

ROC曲线和AUC

模型的泛化能力

模型的泛化能力(generalization ability)是指由该模型对未知数据的预测能力。

过拟合问题！

留出法

我们需要想一个办法，只使用已有的样本数据来对模型的泛化能力进行一个评价。

实际上这个办法很容易想到：还是假设我们现在有 100 个西瓜的数据，这些西瓜的特征数据X以及是否为好瓜Y我们是知道的。

我们只拿出 80 个西瓜来训练我们的“西瓜分类器”，剩下的 20 个西瓜我们假装不知道它们是好瓜还是坏瓜。接下来，我们把这 20 个西瓜的 X 输入到我们的“西瓜分类器”中，来得到预测结果，并和这 20 个西瓜的真实类别进行对比来计算分类准
确率，这个结果就能反映模型的泛化能力的好坏。

我们将这里的 80 个西瓜称为训练集(train set)，它们用来训练我们的模型，得到我们模型中的待估参数；

剩下的 20 个西瓜我们不参与模型的训练过程，只用来最后对模型的好坏进行测试，因此被称为**测试集(test set)**。

我们将上面这种对泛化能力进行评估的方法称为留出法（Hold-Out）。

（1）假设我们总共的样本量为N，我们要将其划分为训练集和测试集，这两个集合的划分比例通常设置为：6:4、7:3 或 8:2。

（2）训练集和测试集的划分既要随机，又要尽可能保持数据分布的一致性（在分类问题中就是类别比例的相似），例如原来 100 个瓜中有 60 个好瓜，40 个坏瓜，那么你按照 8:2 的比例生成训练集和测试集时，尽量保证测试集中的 20 个样本内有 12 个好瓜和 8 个坏瓜。在分类任务中，保留类别比例
的采样方法称为分层采样（stratified sampling）。

留出法的缺陷：在留出法中，用于评价模型泛化能力的测试集只是所有样本的一部分，而且这个结果不是很稳定，对模型的泛化能力的评价依赖于哪些样本点落入训练集，哪些样本点在测试集。

交叉验证

下面我们介绍一种用的更多的方法：k 折交叉验证（K-fold cross-validation）。

我们先将数据集D随机的划分为 k 个大小相似的互斥子集。

每一次用 k-1 个子集的并集作为训练集，剩下的一个子集作为测试集；

这样就可以获得 k 组训练/测试集，从而可进行 k 次训练和测试，最终返回的是这 k 次测试的平均结果，通常 k 取 10，此时称为 10 折交叉验证。

选择最好的模型

我们可以使用决策树、K 最近邻（KNN）、支持向量机（SVM）等常用的机器学习模型。那么，我们应该怎样衡量一个模型的好坏呢？

我们前面介绍了留出法和交叉验证法，这里面都需要将数据分成训练集和测试集。因此，我们可以在同一个训练集下，分别对这些模型进行训练，然后将这些模型分别在测试集上进行预测，并比较不同模型的泛化能力，我们选择泛化能力最好的模型。
（该模型在测试集上的表现最好，例如误差最小，具体的评价指标在前面有介绍）

另外，大多数的模型中都需要设定一些参数(parameter)，参数不同得到的结果可能有很明显的差异。因此，除了要对模型进行选择外，还需要对模型中的参数进行设定，这就是机器学习中常说的“参数调节”或简称“调参”(parameter tuning)。通常调
参依赖于经验，我们后面会介绍网格搜索的方法，来自动搜索使模型效果最好的参数。

1
2
3

重要！！！！！
给定包含 N 个样本的数据集D，在选择模型的过程中，因为需要留出测试集的数 据进行评估测试，所以我们只使用了训练集的数据来训练模型，这会导致测试集的信 息在训练模型的过程中没有被利用到。因此，在模型选择和参数都调整完成后，我们 应该使用完整的数据集 D 来重新训练模型。这个模型在训练过程中使用了所有 N 个样
本，这才是我们最终需要的模型。

欠拟合和过拟合

过拟合（overfitting）指的是模型在训练集上表现的很好，但是在测试集上表现的并不理想，也就是说模型对未知样本的预测表现一般，泛化能力较差。

如果模型不仅在训练数据集上的预测结果不好，而且在测试数据集上的表现也不理想，也就是说两者的表现都很糟糕，那么我们有理由怀疑模型发生了欠拟合（underfitting）现象。

可能产生过拟合的常见原因：

（1）模型中参数设置的过多导致模型过于复杂；

（2）训练集的样本量不够 ；

（3）输入了某些完全错误的的特征

举个极端的例子：样本的编号。现在有 100 个西瓜，编号 1-60 的是好瓜，编号 61-100 的是坏瓜，如果你把编号作为了输入变量放入了我们的模型，那么有可能模型会将编号作为一个最重要的识别变量来对西瓜进行分类，模型会认为只要编号小于等于 60 的都是好瓜，此时在训练集上的误差一定为 0。。。。。。如果这时候你拿来编号大于 100 的需要判断好坏的瓜，模型都会认为是坏瓜！

解决过拟合的方法：

（1）通过前面介绍的交叉验证的方法来选择合适的模型，并对参数进行调节。

（2）扩大样本数量、训练更多的数据

（3）对模型中的参数增加正则化（即增加惩罚项，参数越多惩罚越大）

欠拟合则和过拟合刚好相反，我们可以增加模型的参数、或者选择更加复杂的模型；也可以从数据中挖掘更多的特征来增加输入的变量，还可以使用一些集成算法（如装袋法（Bagging），提升法（Boosting））。

（注意：有可能模型的输入和输出一点关系都没有，举个极端的例子，你买的西瓜好坏和你的个人特征没任何关系，例如你的性别身高体重等）

常见的机器学习算法的思想

五分钟机器学习的个人空间_哔哩哔哩_bilibili

菊安酱的个人空间_哔哩哔哩_bilibili

K最近邻（KNN）

决策树（Decision Tree）

支持向量机（SVM）

线性支持向量机

非线性支持向量机

集成学习（ensemble learning）

Matlab中机器学习的应用

蒙特卡洛

引例：布丰投针

通过针与平行线中任意一条相交的概论，计算pi
axis：绘制坐标在的框架

蒙特卡洛概述

蒙特卡洛方法又称统计模拟法，是一种随机模拟方法，以概率论和数理统计方法为基础的一种计算方法，是使用随机数来解决很多计算问题的方法。
原理：由大数定理可知，当样本容量足够大的时候，事件的发生频率即其概率
蒙特卡洛不是一种算法，而是一种方法，蒙特卡洛没有固定的通用代码。

蒙特卡洛是枚举的一种变异

应用1 三门问题

三门问题（Monty Hall problem）亦称为蒙提霍尔问题、蒙特霍问题或蒙提霍尔悖论，大致出自美国的电视游戏节目Let’s Make a Deal。问题名字来自该节目的主持人蒙提·霍尔（Monty Hall）。参赛者会看见三扇关闭了的门，其中一扇的后面有一辆汽车，选中后面有车的那扇门可赢得该汽车，另外两扇门后面则各藏有一只山羊。当参赛者选定了一扇门，但未去开启它的时候，节目主持人开启剩下两扇门的其中一扇，露出其中一只山羊。主持人其后会问参赛者要不要换另一扇仍然关上的门。问题是：换另一扇门是否会增加参赛者赢得汽车的机率。如果严格按照上述的条件，那么答案是会。不换门的话，赢得汽车的几率是1/3。换门的话，赢得汽车的几率是2/3。
虽然该问题的答案在逻辑上并不自相矛盾，但十分违反直觉。这问题曾引起一阵热烈的讨论。
李永乐，三门问题

应用2 模拟排队问题

指数分布

normrnd()——正态分布
exprnd()——指数分布

tic
代码
toc
计算代码运行的时间

应用3 有约束的非线性规划问题

非线性规划——局部最优解，计算时需要初始值
全局最优解是计算不出来的！

把约束条件使用放缩法，计算出每个变量的取值范围

format long g——计算出的结果，显示更多的小数位数
x=unifrnd(20,30,n,1):生成[20,30]之间均匀分布的随即数组成的n行1列的向量构成x

应用4 01规划问题

unique函数：剔除一个矩阵或者向量的重复值，并将结果按照从小到大的顺序排列

循环进行超级多次，得到最优解

应用5 导弹追踪问题

连续的时间离散化
mod(8,3):求余数

应用6 旅行商问题（TSP）

n数值过大的时候，可能出现的次数将达到非常大的量级

randperm函数：随即序列

http://www.math.uwaterloo.ca/tsp/

数学规划模型

数学规划：数学规划三运筹学的一个分支，期用来研究：在给定的条件下（约束条件），如何按照某一衡量指标（目标函数）来寻求计划，管理工作中的最优方案，即求目标函数在一定约束条件下的极值问题！

数学规划的一般形式

概念

数学规划的分类

线性规划
目标函数和约束条件是决策变量的线性表达式
单纯形法
非线性规划
目标函数或者约束条件是决策变量的非线性表达式
没有通用算法，大多数算法都是选定决策变量的初始值之后，通过一定的搜索方法，寻找最优的决策变量
整数规划
要求变量取整数的数学规划，分为线性整数规划和非线性整数规划
求解线性整数规划问题能求解
非线性整数规划——蒙特卡洛模拟
0-1 规划
重点内容

线性规划问题的求解——matlab

Matlab中线性规划的标准型

matlab中求解线性规划的命令
[x,fval] = linprog[C,A,b,Aeg,beg,lb,ub,x0]

% [x fval] = linprog(c, A, b, Aeq, beq, lb,ub, x0)  
% c是目标函数的系数向量，A是不等式约束Ax<=b的系数矩阵，b是不等式约束Ax<=b的常数项
% Aeq是等式约束Aeq x=beq的系数矩阵，beq是等式约束Aeq x=beq的常数项
% lb是X的下限，ub是X的上限，X是向量[x1,x2,...xn]' , 即决策变量。
% 迭代的初始值为x0（一般不用给）