信号与系统
信号与系统是很重要的一门课,是很多学校通信考研的专业课!
这门课几乎每个知识点都很重要,最重要的是三大变换:傅里叶变换,拉普拉斯变换,Z变换。
学好这门课在课本理解和做题两方面都需要抓紧!
信号与系统在我学的科目中属于做题比较多的了,我自我感觉,对于定义的理解和对于基本题型的解答都还是不错的,但是期末用事实告诉我,我做的该不够!
特别的对于基本知识点的理解和对定义的掌握不好,导致在期末做题的时候对于题目表达的意思我理解起来都很吃力!
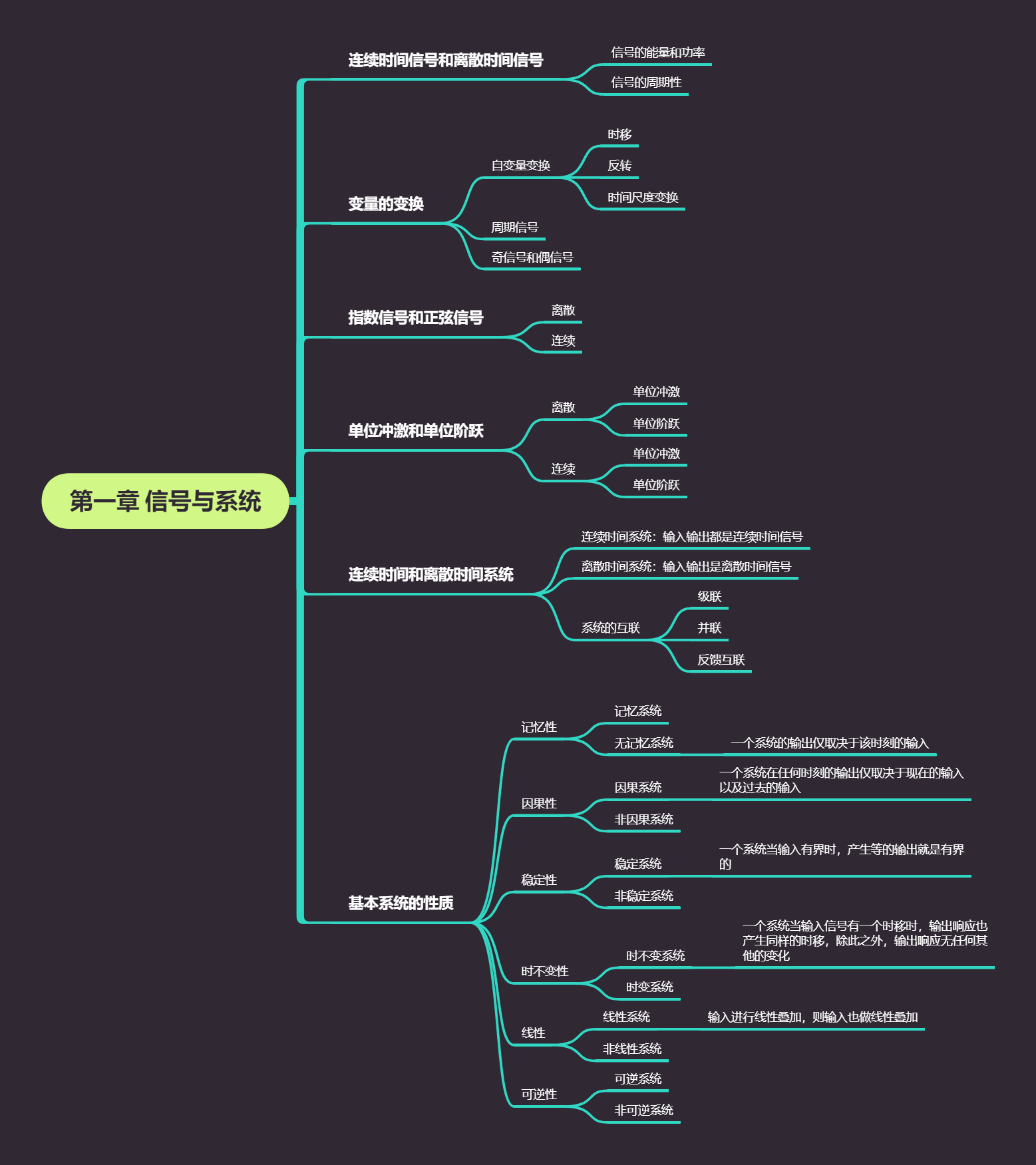
第一章 信号与系统
1 | |
1.0 引言
信号
- 信号的定义:描述一定物理现象
- 信号的表示方式:函数
- 信号的分类、
- 确知信号和随机信号
- 连续时间信号和离散时间信号
信号与系统不是讲数学,而是用数学的方法来解决信号处理的问题
1.1 连续时间信号和离散时间信号
1.1.1 数学表示
连续时间信号(CTS):自变量是连续可变的
离散时间信号(DTS):仅仅定义在离散时刻点上
连续时间信号->离散时间信号?
- 连续时间信号在离散时刻点上的样本可以构成一个离散时间信号(采样)
1.1.2 信号的能量与功率
能量
平均功率
有限区间内CTS和DTS的总能量和平均功率的计算
无限区间内CTS和DTS的总能量和平均功率的计算
利用能量与功率将信号分为三类:
- 能量信号——信号具有有限的总能量
- 信号的总能量有限
- 平均功率为0
- 功率信号——信号具有无限的总能量但是平均功率有限
- 信号的总能量有限
- 平均功率为大于0,小于∞
- 非能量信号也非功率信号
- 信号的总能量无穷大
- 信号的平均功率无穷大
1.1.3 周期信号与非周期信号
$$
x(t)=x(t+nT)
$$
$$
x[n]=x[n+N]
$$
周期信号一定是功率信号
非周期信号,且能量有限的信号称为能量信号
1.2 自变量的变换
自变量的变换必然会使得信号的特性相应地改变
1.2.1 自变量变换
时移变换 shift of signals
- 左加右减
时间反转 time reversal
- 以纵轴为轴呈镜像对称
时间尺度变换 time scaling
- 在时间常数上对时间做压缩或者扩展
1.2.2 周期信号
周期:T或N
基波周期:$T_0$或$N_0$
1.2.3 偶信号和奇信号
任何一个信号都能分解成两个信号之和,其中之一为偶信号,另一个为奇信号。
1.3 指数信号和正弦信号
1.4 单位冲激和单位阶跃函数(重要)
离散时间的单位脉冲和单位阶跃序列
连续时间单位冲激和单位阶跃函数
课本P19——重要内容

1.5 连续时间和离散时间系统
1.6 基本系统的性质

第二章 线性时不变系统
离散线性时不变系统

连续时间线性时不变系统

线性时不变系统的性质

第三章 周期信号的傅里叶级数表示
线性时不变系统对复指数信号的响应

连续时间周期信号的傅里叶级数表示
成谐波关系的复指数信号的线性组合

连续时间周期信号傅里叶级数表示

傅里叶级数收敛

连续时间傅里叶级数性质
线性性质

时移性质

时间反转
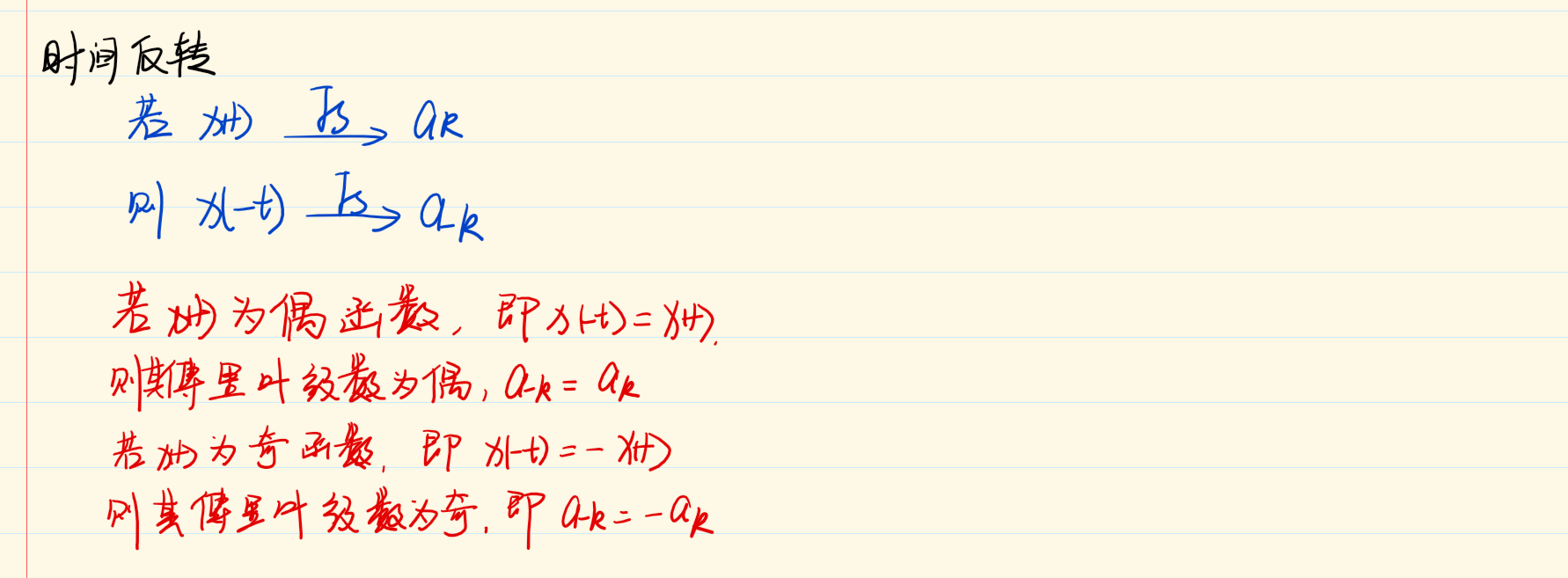
时间尺度
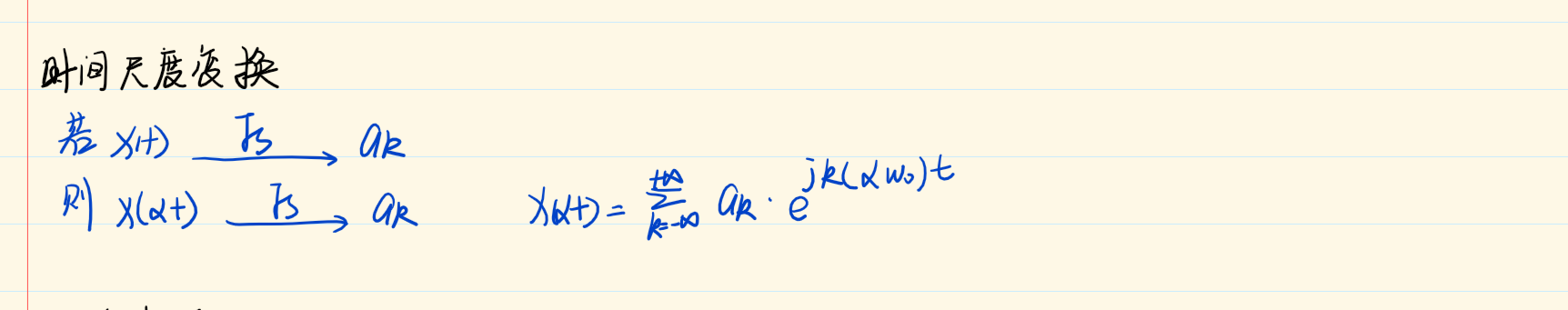
相乘性质
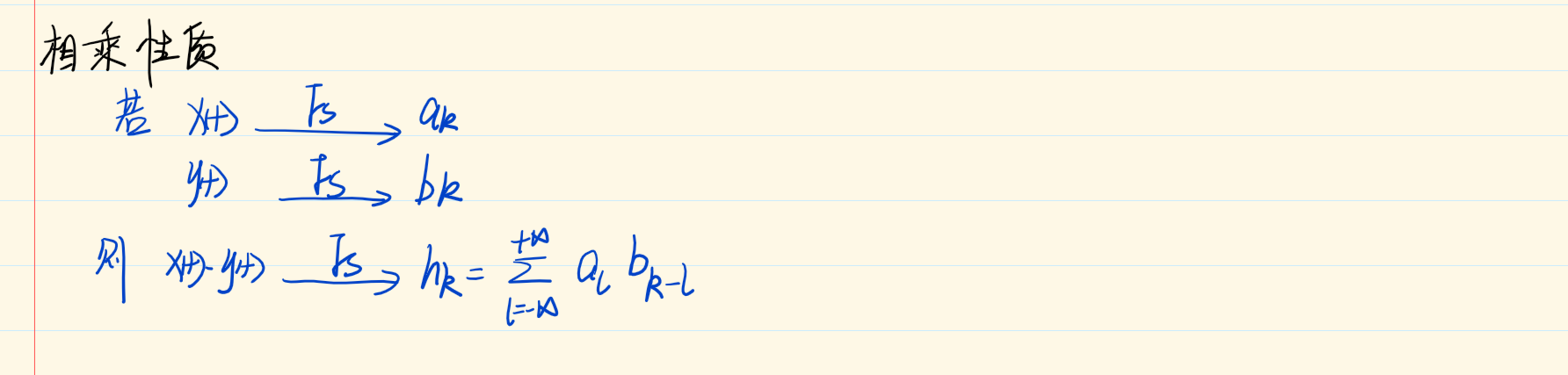
共轭及其共轭对称

连续时间周期信号的帕斯瓦尔定理

总结:连续时间傅里叶级数性质

第四章 连续时间傅里叶变换
4.1非周期信号的表示

傅里叶变换的收敛

常见傅里叶变换举例子
4.2周期信号的傅里叶变换
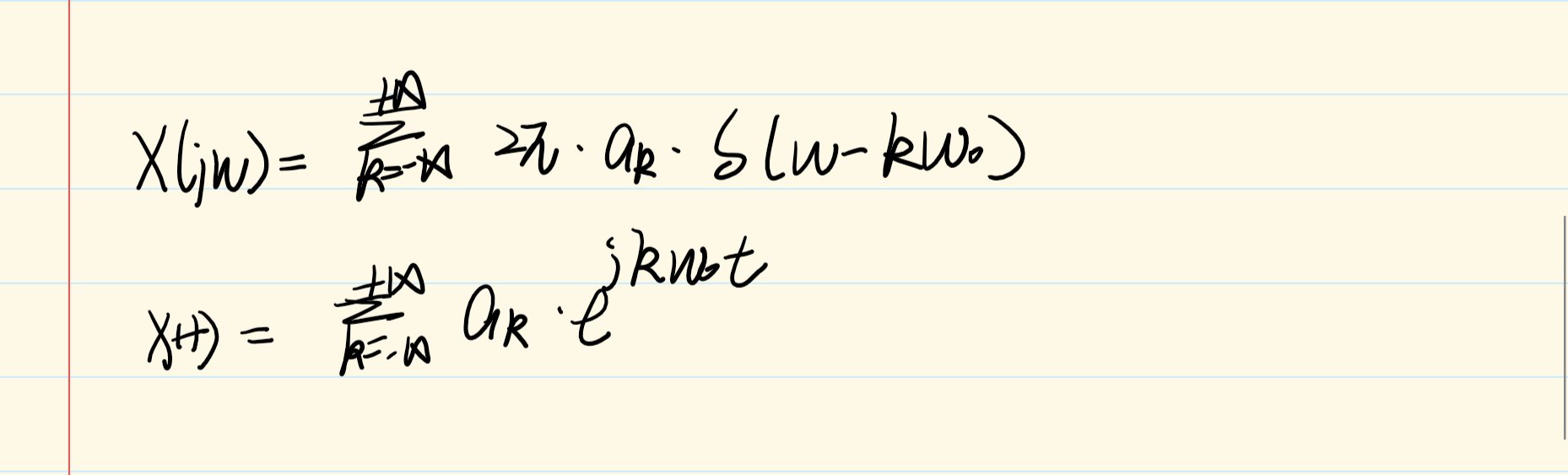
4.3连续时间傅里叶变换性质
线性性质

时移性质
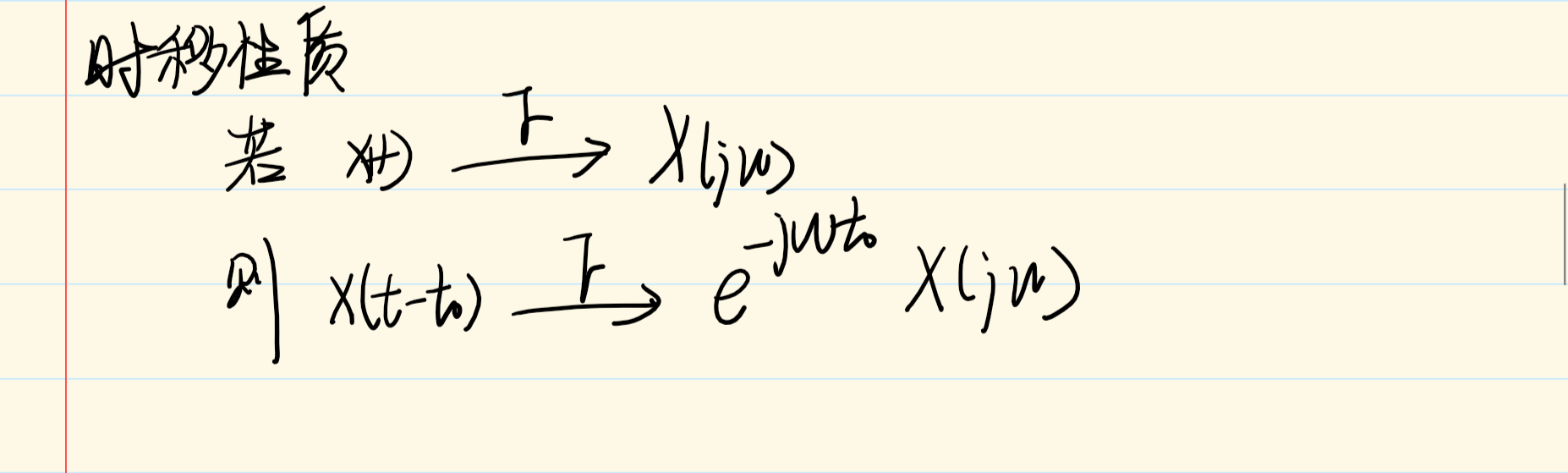
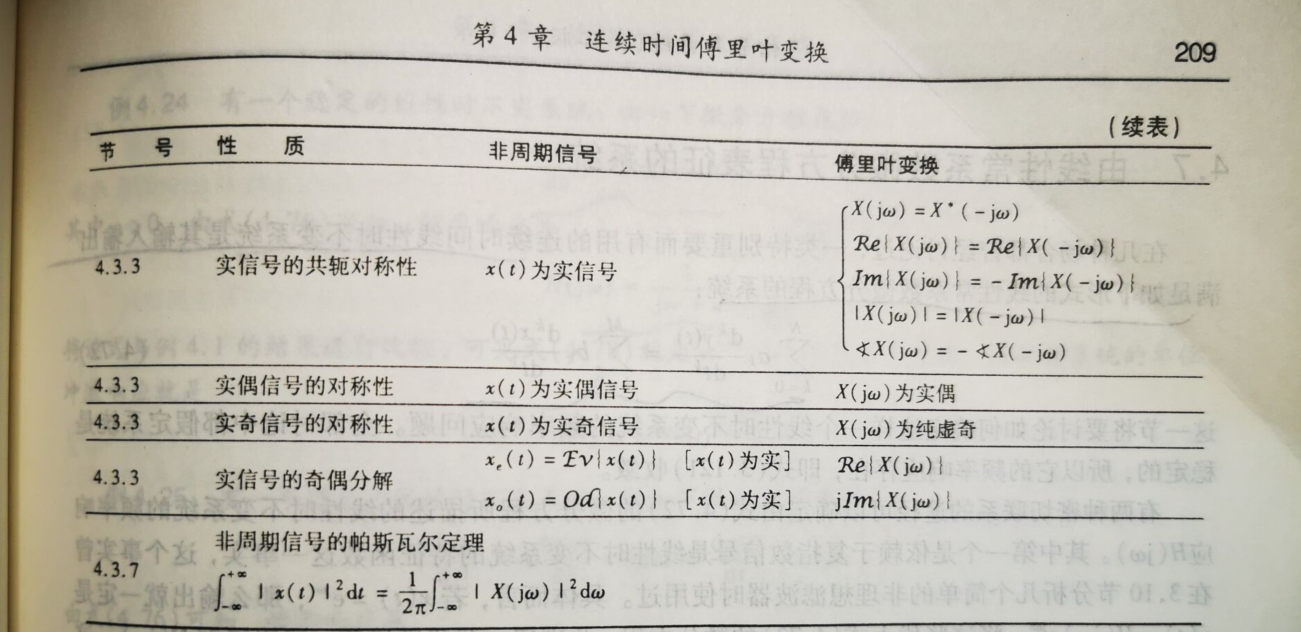
共轭和共轭对称性质
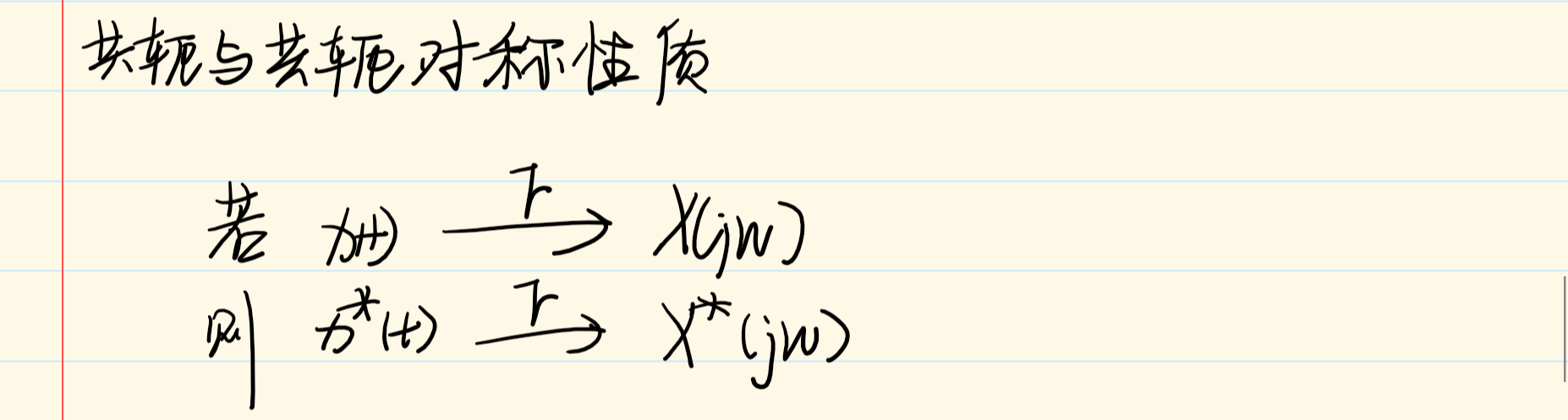



微分与积分性质

时间与频率的尺度变换

对偶性质
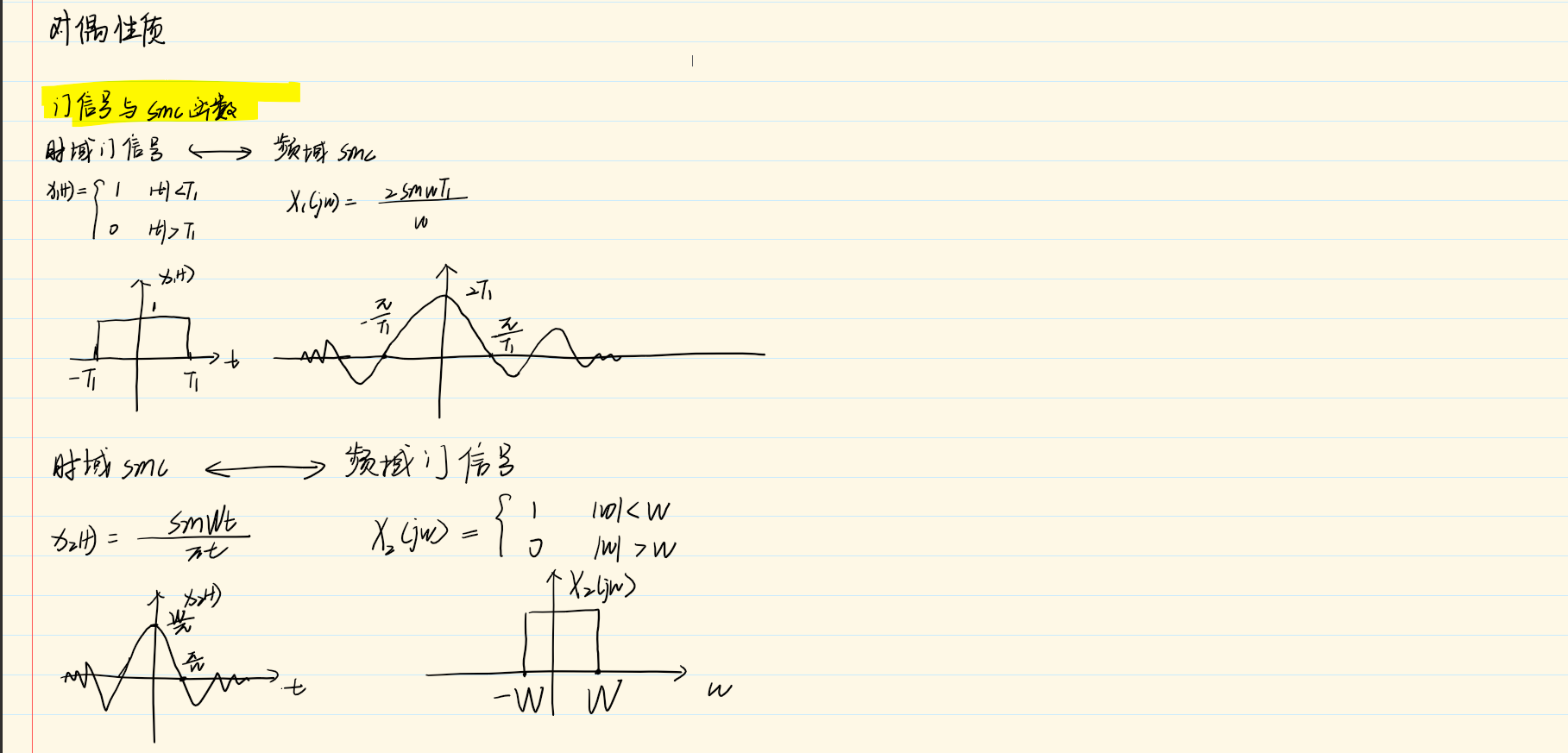

帕斯瓦尔定理
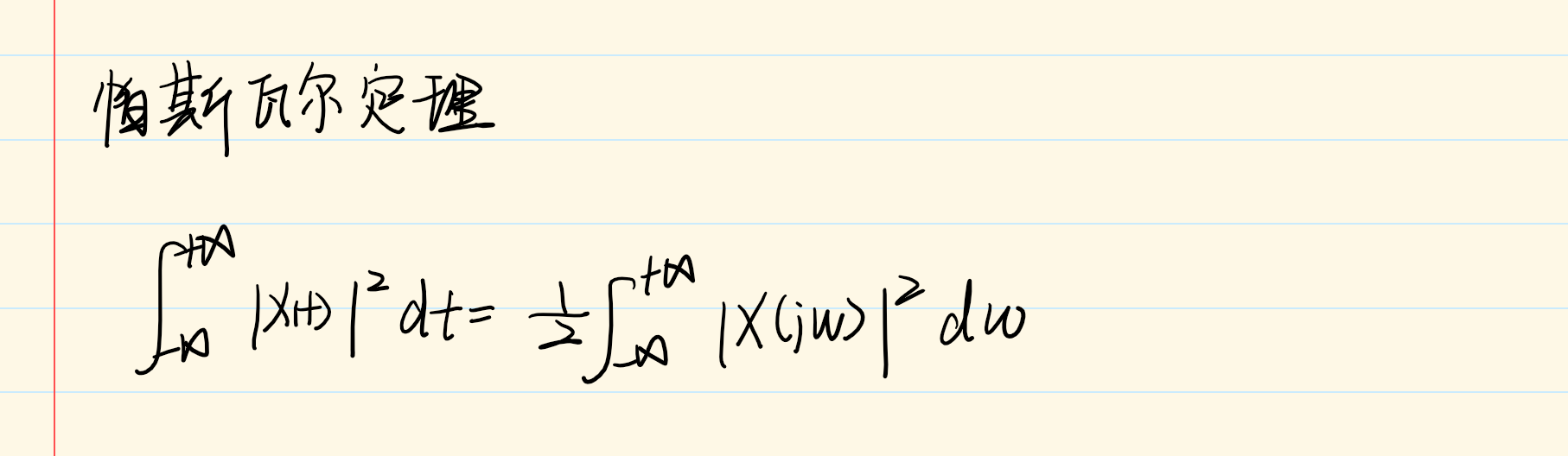
4.4 卷积性质

4.5 相乘性质
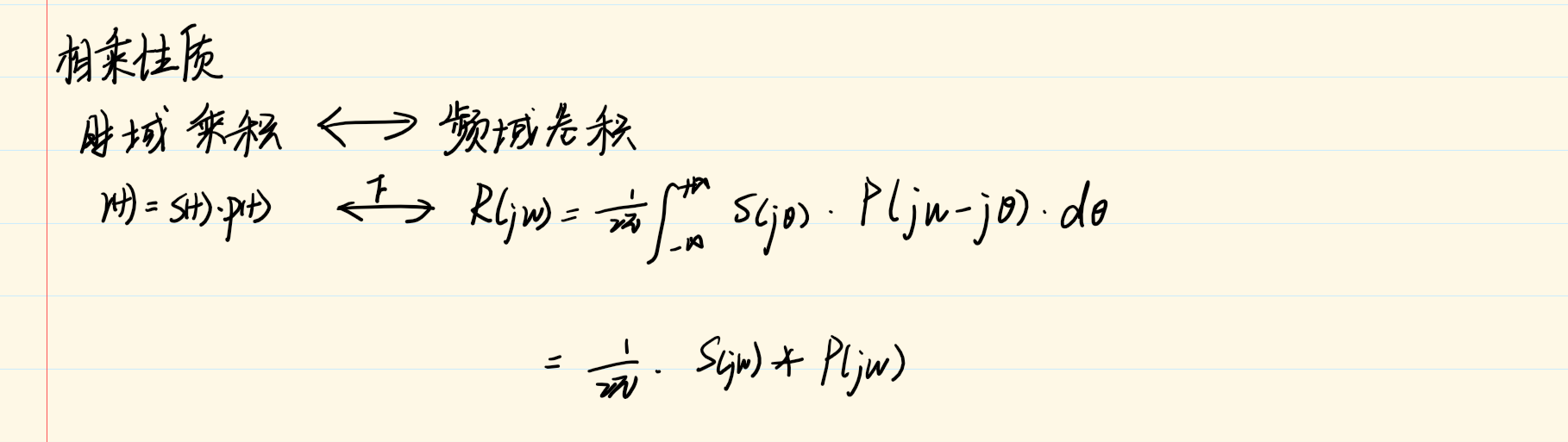


第五章 离散时间傅里叶变换

.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
第六章 信号与系统的时域和频域特征
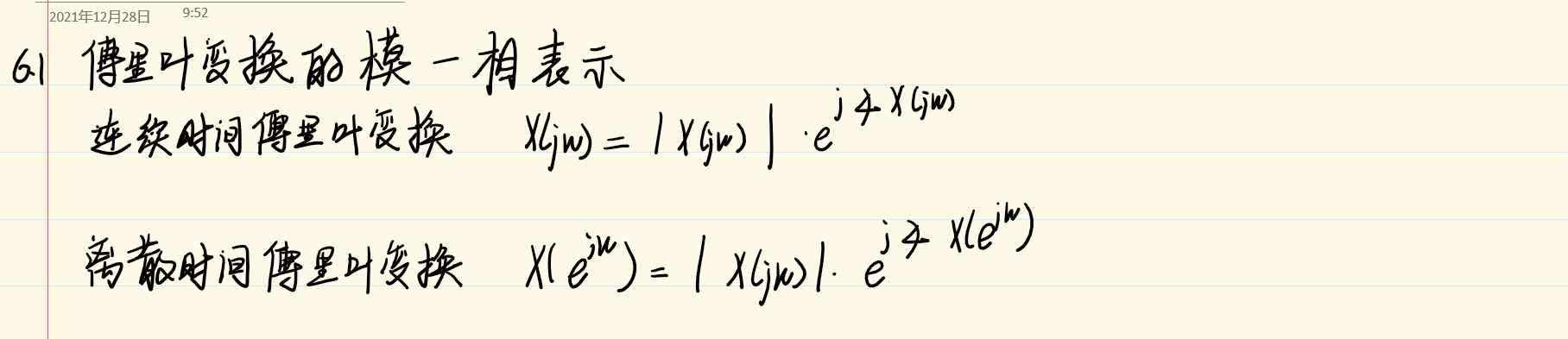
6.2 线性时不变系统频率响应的模和相位表示

群时延

对数模和相位图

6.3 理想频率选择器滤波器的时域特性


6.5 一阶连续时间系统

第七章 采样
7.1 用信号样本表示连续时间信号:采样定理

冲击串采样




零阶保持采样

7.2 利用内插由样本重建信号

7.3 欠采样的效果:混叠现象

7.4 连续时间信号的离散时间处理
7.5 离散时间信号采样
第八章 通信系统
8.0 引言

8.1 复指数载波




8.2 正弦载波
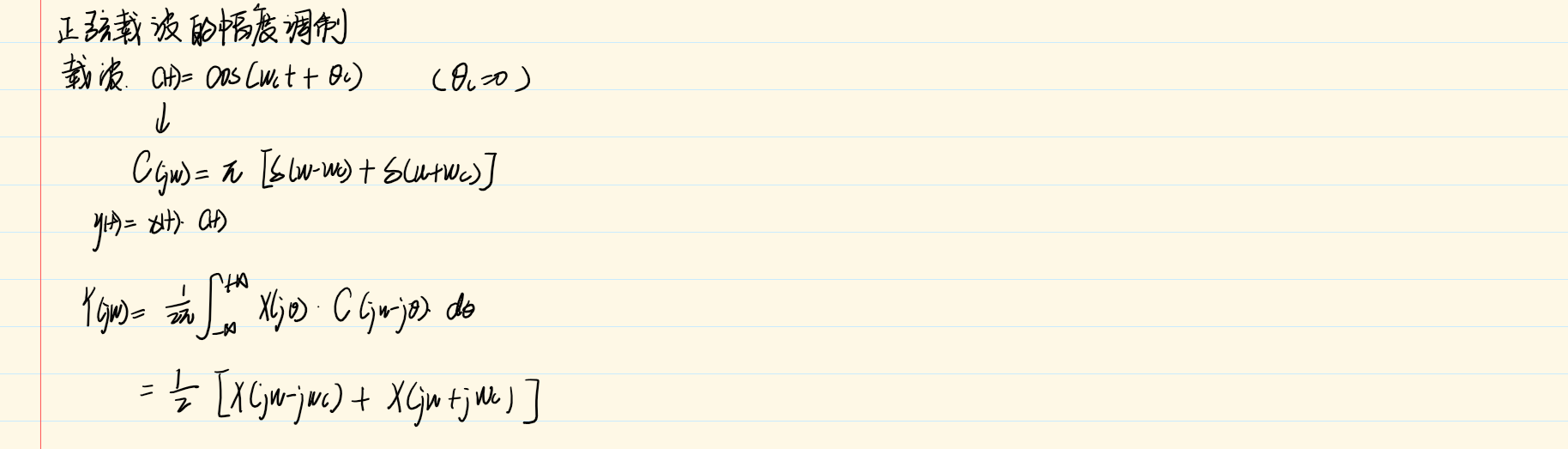

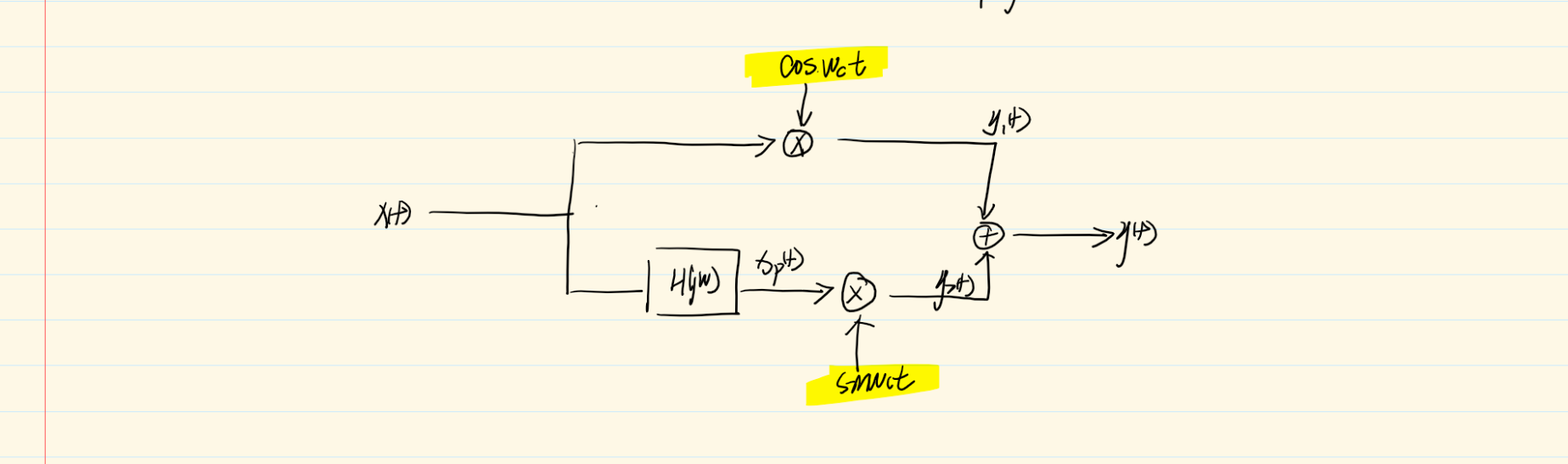
解调




8.3 频分多路复用

8.4 单边带正弦幅度调制



第九章 拉普拉斯变换
9.0 引言
连续时间傅里叶变换的推广——拉普拉斯变换
拉普拉斯变换和Z变换能用于很多不稳定系统的分析
9.1 拉普拉斯变换



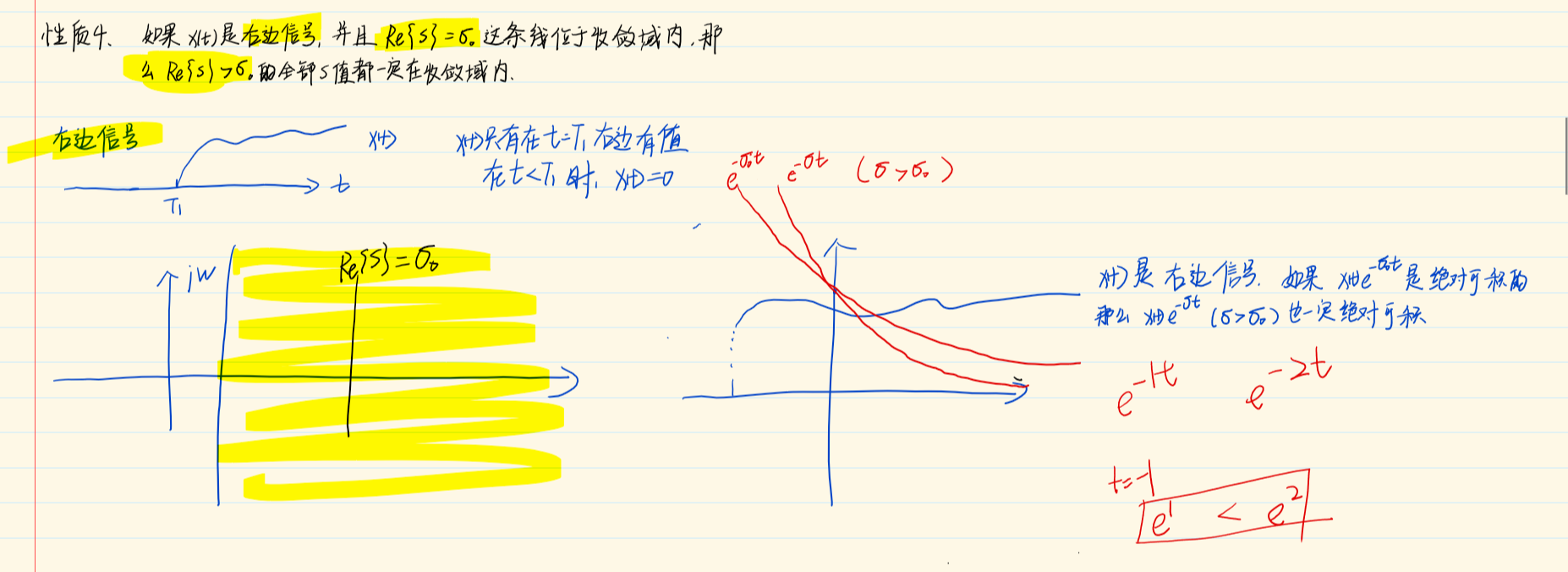
9.2拉普拉斯变换的收敛域







9.3 拉普拉斯逆变换

部分分式展开


部分分式展开——重根的情况
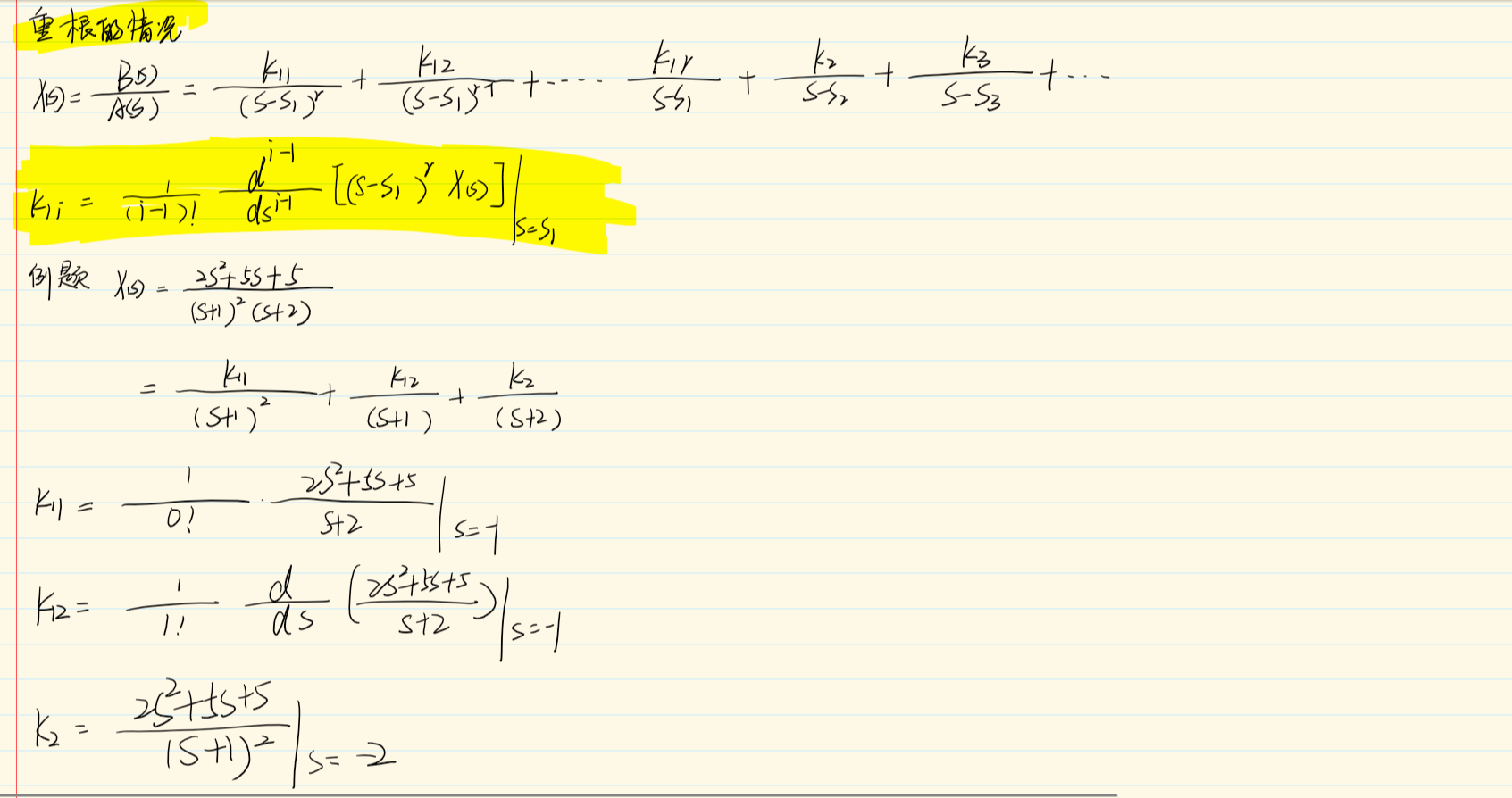
9.4 由零-极点图对傅里叶变换进行几何求值

9.5 拉普拉斯变换的性质

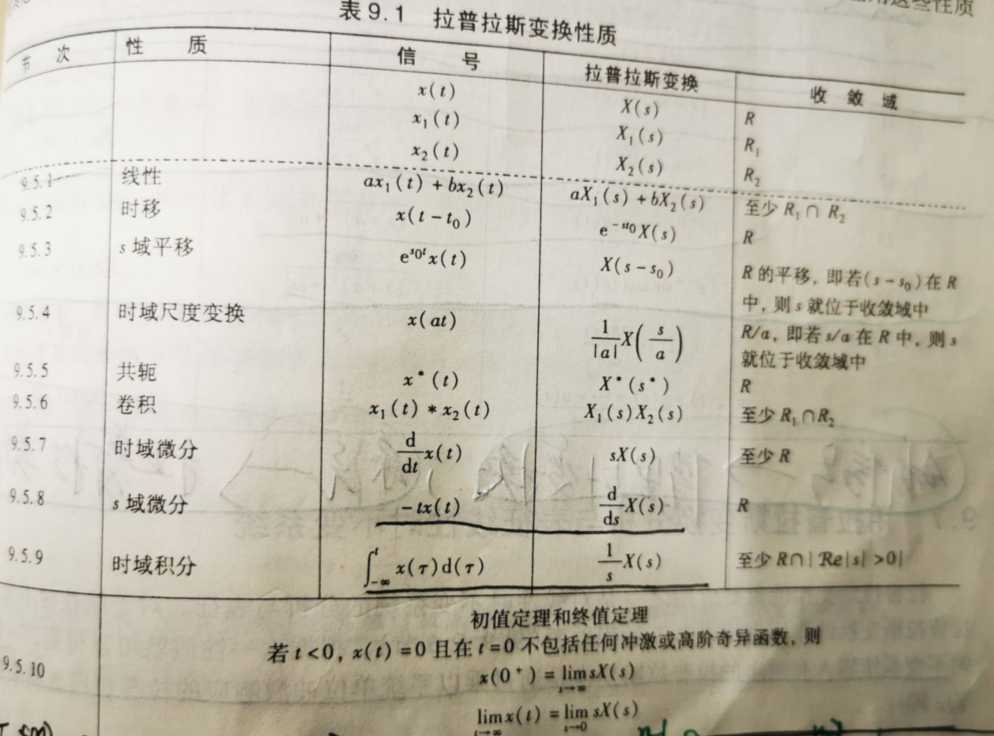
9.6 常用拉普拉斯变换对


9.7 用拉普拉斯变换分析表征线性时不变系统



9.8 系统函数的代数属性与方框图表示

9.9 单边拉普拉斯变换





第十章 Z变换
10.1 z变换




10.2 z变换的收敛域




10.3 z逆变换

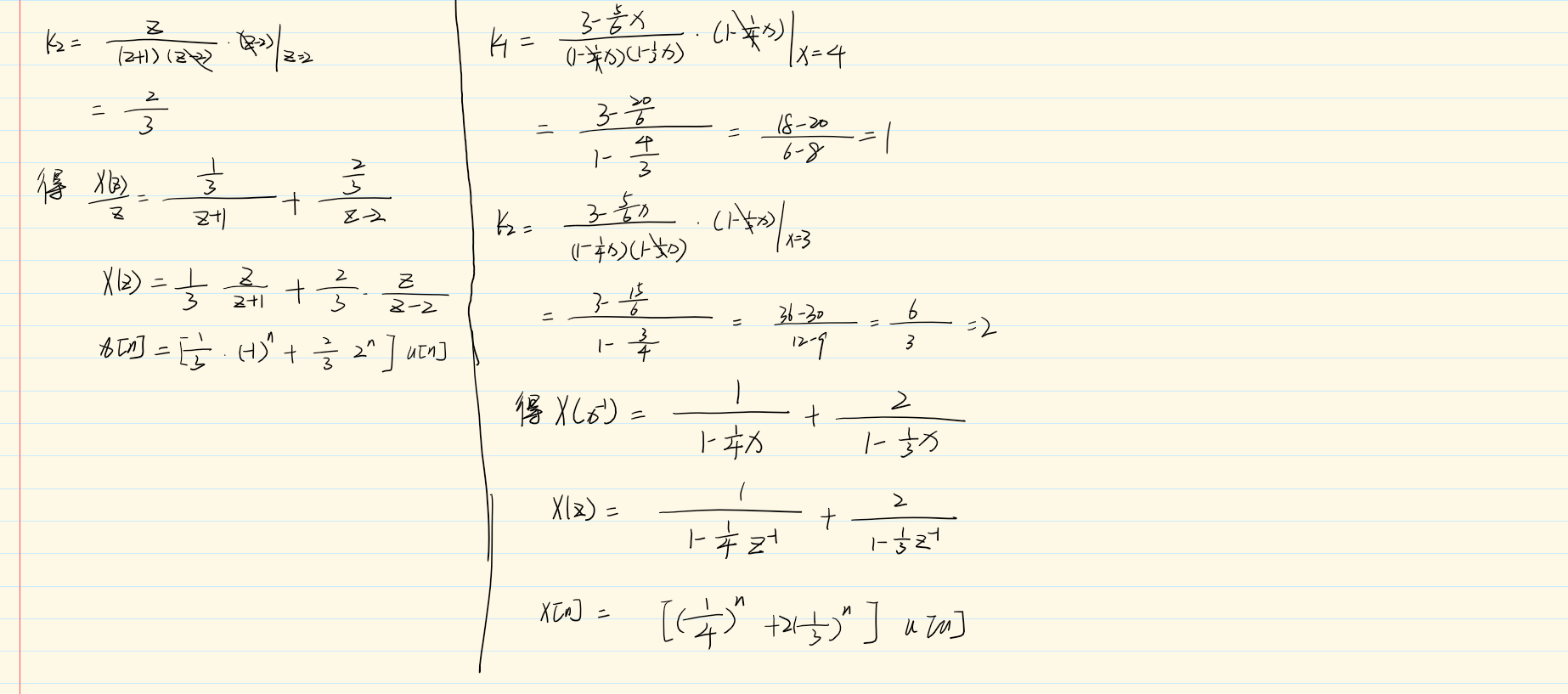
10.4 利用零极点图对傅里叶变换进行几何求值
一阶系统
二阶系统(可能要考)
10.5 z变换的性质



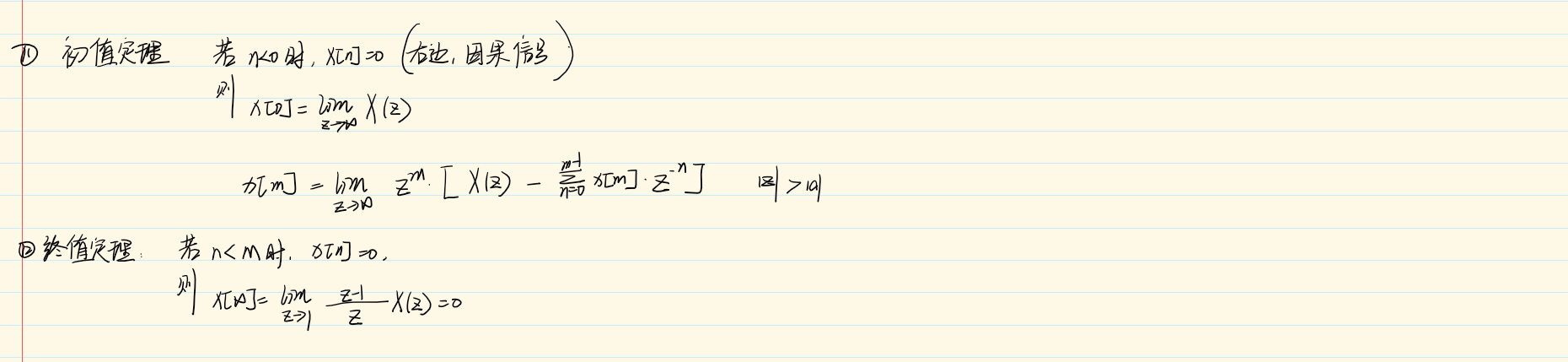
10.6 常见z变换对

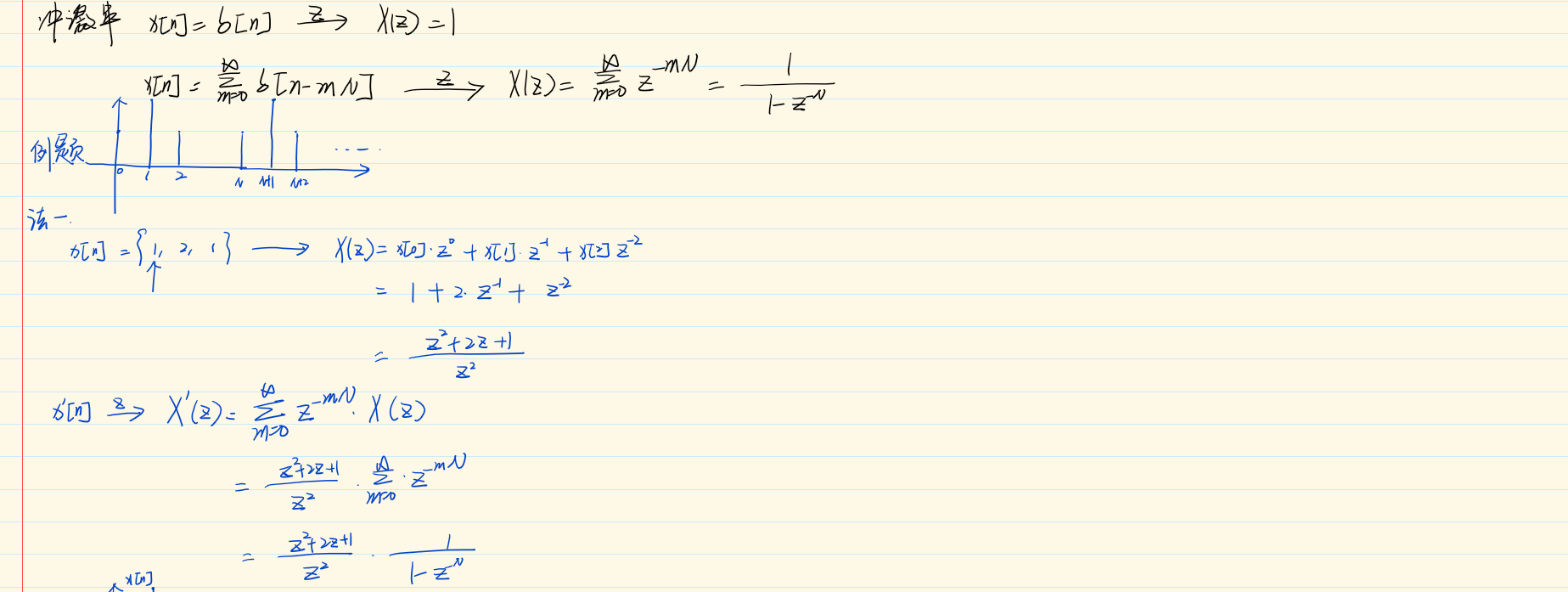
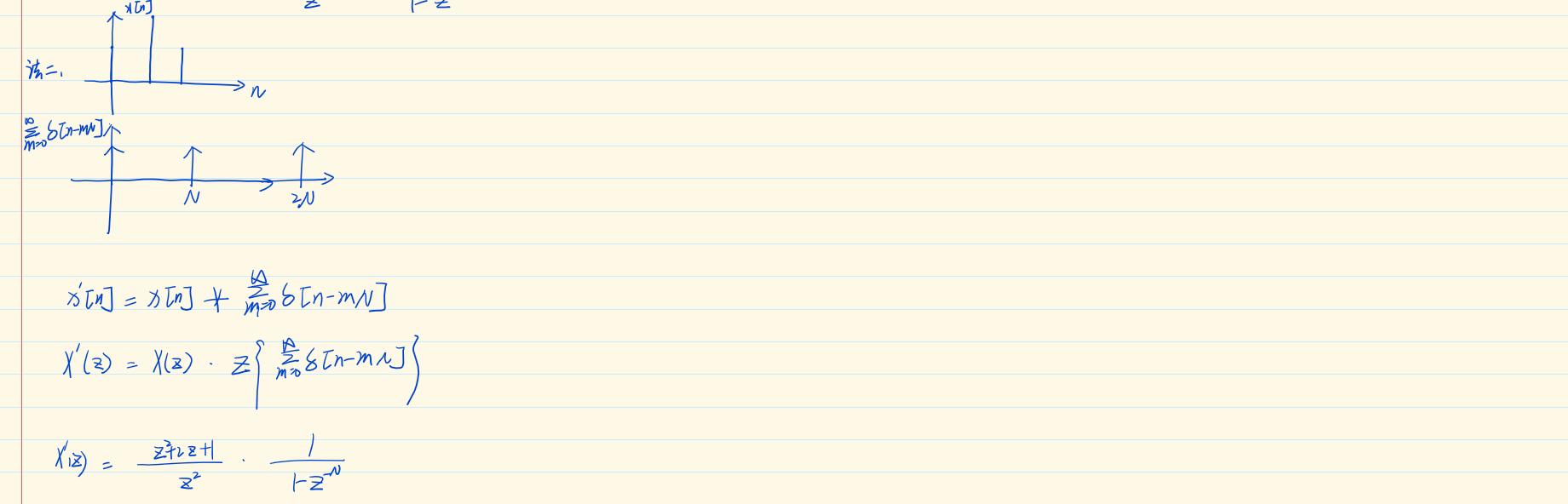

10.7 利用z变换分析与表征线性时不变系统




10.8 系统函数的代数属性与方框图表示
10.9 单边z变换



信号与系统
https://cosmicdusty.cc/post/Knowledge/SignalsAndSystems/