信息论
这门课学的过程很痛苦,太多定义了,到期末的时候完全不懂,即使已经复习完了前四章的知识点,但是对基本的定义都没有掌握,因此复习到第四章感觉效果很差,我果断放弃了自己看课本理解,而是去找了一个老师讲课的视频,跟着老师串了一遍课本知识,老师在讲课的时候也给出了很多的例题!这个视频是北邮杨洁老师录制的B站:北邮杨洁老师
第一章 绪论
信息的定义
1 | |
物质世界的三大支柱:物质,信息,能量
区分定义:
信息:事物运动状态或存在方式的不确定性的描述
消息:含有信息的语言,文字,图像等
信号:
- 信息的物理层表示,传递信息的载体
- 消息的物理体现,光、点信号等
信息的特征
- 不确定性:接收者在收到信息之前,对它的内容是不知道的
- 信息可以使认识主体对某一事物的未知性或不确定性减少
- 信息是可以度量的
信息论所研究的对象:
1 | |
噪声源:主要干扰信道
信息论研究的目的
- 可靠性$\stackrel{信道编码}{\longrightarrow}$多冗余
- 有效性$\stackrel{信源编码}{\longrightarrow}$少冗余
- 保密性
- 认证性
信息论的研究内容
- 狭义的信息论/经典信息论/香农基本理论
- 信息的测度
- 信道容量
- 信源编码
- 信道编码
- 一般信息论/工程信息论
- 广义信息论
香农信息论的建立和发展
香农信息论的核心
1 | |
- 无失真信源编码定理
- 信道纠错编码
- 限失真信源编码定理
- 多用户、网络信息论的发展
- 信息保密与安全定理
第二章 离散信源及其信息测度✔
2.1 信源的数学模型及其分类
信源是信息的来源,是产生消息或消息序列的源泉。
信息是抽象的,而消息是具体的。
消息不是信息本身,但它包含着和携带这消息。
我们研究的是信源各种可能的输出以及输出各种可能消息的不确定性。
信源的描述:用一个样本空间及其概率测度,也就是概率空间/信源空间。
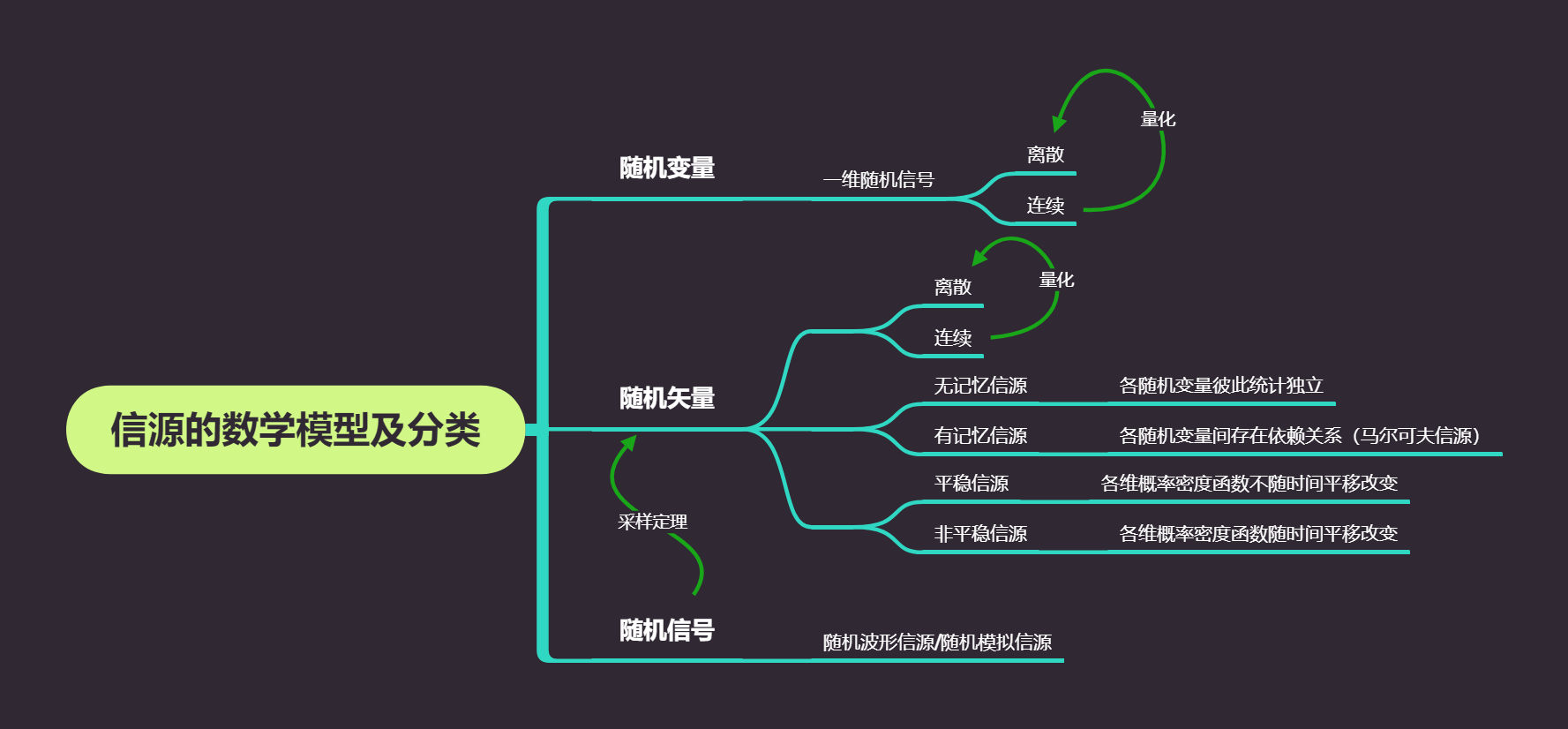
根据消息的不用的随机性质来对信源进行分类:
- 信源输出的消息用随机变量描述
- 信源可能输出的消息是有限的或可数的,并且每次只输出其中一个消息。
- 信源的概率空间必定是一个完备集;

- 信源输出的消息用随机矢量描述
- 信源输出的消息用随机过程描述

2.2 离散信源的信息熵
- 信息量的定义:
收到某信息获得的信息量(即收到某信息后获得关于某基本事件发生的信息量)
= 不确定性减少的量
= (收到此消息前关于某事件发生的不确定性)-(收到此消息后关于某事件发生的不确定性)
无噪声的情况下:收到某消息获得的信息量=收到消息前关于事件发生的不确定性=信源输出的某消息中所含有的信息量

信息量是事件发生的先验概率的函数——自信息量
信息量的单位
- 以2为底:bit
- 以e为底:nat
- 以10为底:hart
- 换底公式
信息熵
自信息是信源发出某一消息所含有的信息量,信源所发出的消息不同,所含有的信息量也就不同。自信息就是一个随机变量,不能用来作为整个信源的信息测度
信息熵——信源的平均自信息:自信息的数学期望
单位:bit/符号——nat/符号——hart/符号
信息熵的物理含义
- 表示信源输出后,每个消息(符号)所提供的平均信息量
- 表输信源输出前,信源的平均不确定性
- 用来表征变量X的随机性
2.3 信息熵的基本性质
概率矢量——熵函数


2.5 离散无记忆信源的扩展信源



2.6 离散平稳信源
联合熵
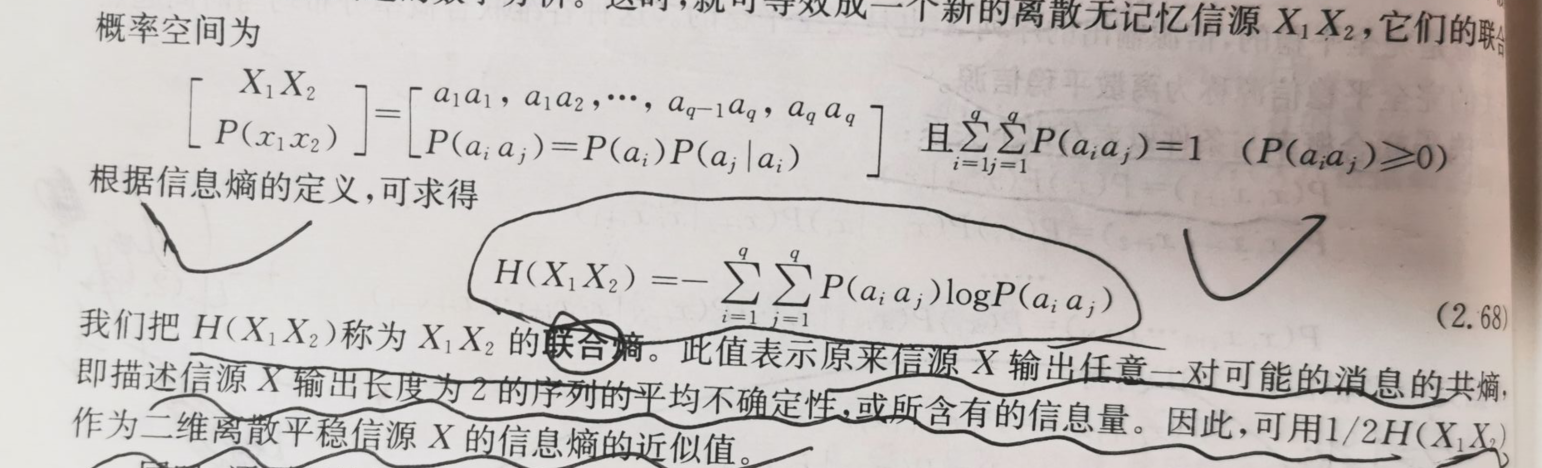
条件熵
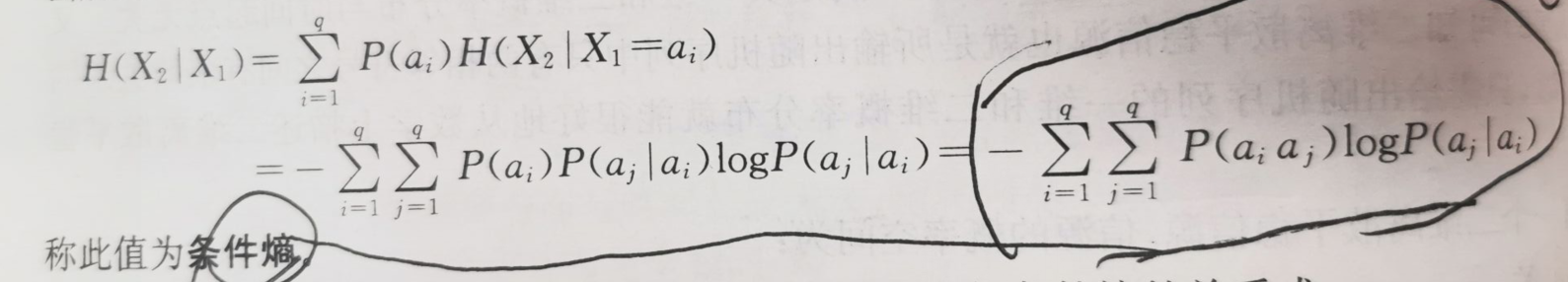
贝叶斯公式

有限定条件的熵小于无限定条件的熵
熵的强可加性


离散平稳信源的极限熵


使用条件熵近似极限熵

记忆长度为m(即某时刻输出什么符号只能与前m个符号有关),则得离散平稳信源得极限熵等于有限记忆长度为m的条件熵

2.7 马尔可夫信源
马尔可夫信源——非平稳有记忆信源
未来不依赖于过去的演变,只取决于现在
有许多信源是非平稳信源,但在其输出的符号序列中符号之间的依赖关系是有限的

马尔可夫信源的定义

m阶马尔可夫信源

状态转移图与一次转移概率

时齐,遍历的马尔可夫信源的熵
时齐,遍历的m阶马尔可夫信源的熵

2.8 信源剩余度与自然语言的熵



第三章 离散信道及其信道容量✔
1 | |
3.1信道的数学模型及其分类



二元对称信道

二元删除信道

四种概率


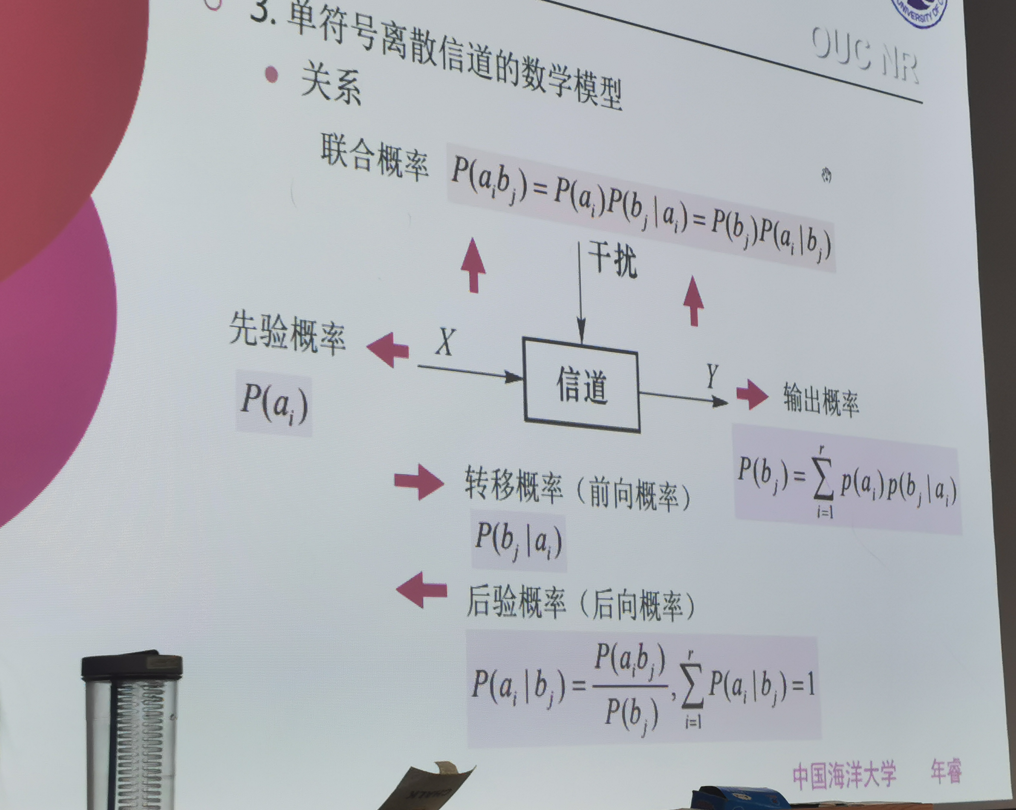
3.2平均互信息及平均条件互信息
四种熵


平均互信息







条件互信息

平均条件互信息

3.3平均互信息的特性

3.4信道容量及其一般计算方法
信道容量


无噪无损一一对应信道

有噪无损信道

无噪有损信道(确定信道)

对称离散信道

准对称信道


一般离散信道


(这个定理不懂)
3.6离散无记忆扩展信道及其信道容量





3.7 独立并联信道及其信道容量



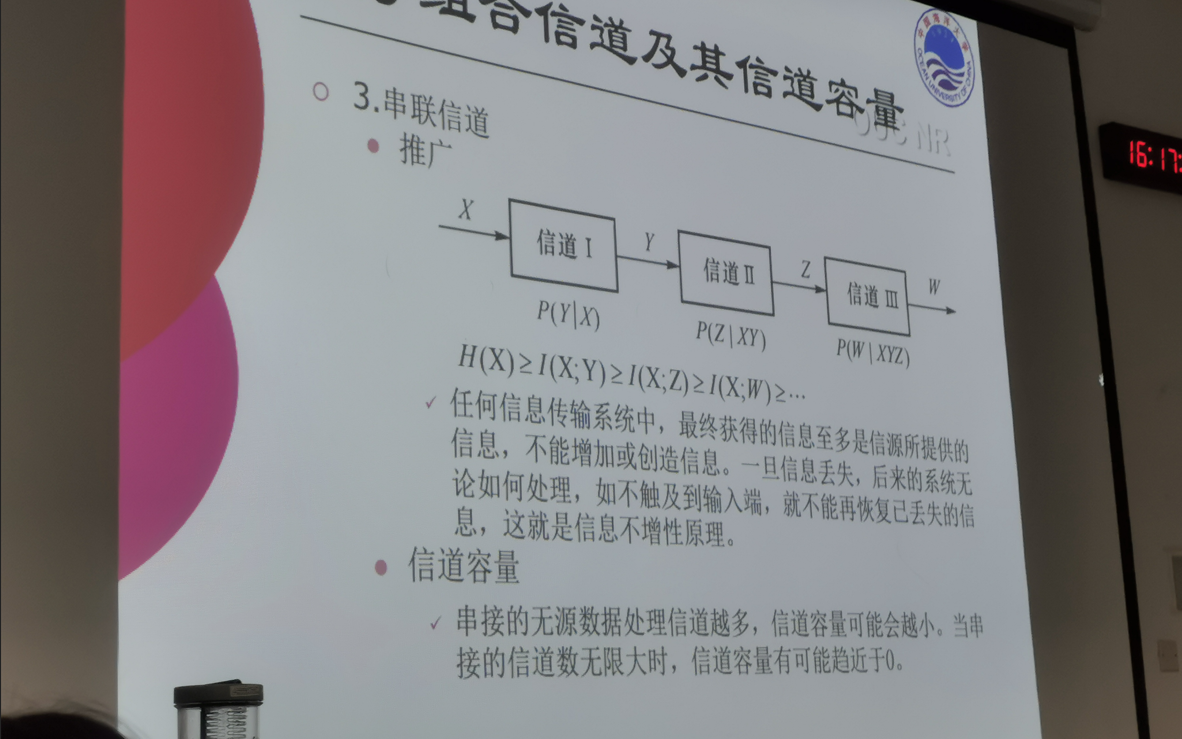
3.8 串联信道的互信息和数据处理定理


3.9 信源与信道匹配

第四章 波形信源和波形信道
1 | |
4.1 波形信源的统计特性和离散化
随机波形信源输出的消息是随机的,因此,可以用随机过程{x(t)}来描述;
- 随机波形信源中的消息数是无限的;
- 对于随机波形信源,也用有限维概率密度函数族及与各维概率密度函数有关的统计量来描述;
就其统计特性来分类:平稳随机过程——非平稳随机过程
- 平稳随机过程:各维概率密度函数不随时间平移而发生变化的随机过程;
- 非平稳随机过程:


4.2连续波形信源和波形信源的信息测度
差熵


连续平稳信源的差熵


波形信源的差熵

特殊连续信源1——均匀分布连续信源的差熵



特殊连续信源2——高斯信源的差熵


4.3 连续信源熵的性质及最大差熵定理
可加性

上凸性

差熵可取负值

变换性

极值性(最大差熵定理)


峰值功率受限条件下信源的最大熵

平均功率受限条件下信源的最大熵


4.4 连续信源熵的变换
4.5 熵功率⭐(不是很懂)





4.6 连续信道和波形信道的分类






4.7 连续信道和波形信道的信息传输律
基本连续信道

多维连续信道

波形信道

连续信道平均互信息的特性



