电磁场与电磁波
电磁场与电磁波,这门课有点难,难就难在太多公式了!
前半部分是电磁场部分,与大学物理所学的东西有很多重合的地方,因此老师在讲课的时候,回默认大家的大学物理电磁场学的很好,我的大学物理学的并不好,因此电磁场部分学的很吃力,很多知识点都听不太懂,记不住!
后半部分是电磁场部分,知识点不多,记住基本的条件下的电磁波就能理解特殊的条件下的电磁场吧,这一部分问题也是公式太多了,特别是引入的复矢量,对定义的理解一下子就难了起来了!
这门课要想学好,得刷题,记忆公式!
绪论

第一章 矢量分析
矢量加减法
矢量乘法
1标量与矢量的乘积
- 结果为矢量
2矢量与矢量的标量积(点乘)
- 结果为标量

3矢量与矢量的矢量积(叉乘)
- 结果为矢量
- 结果矢量的方向满足右手螺旋定则

4三矢量的乘积
- 标量三重积

- 矢量三重积

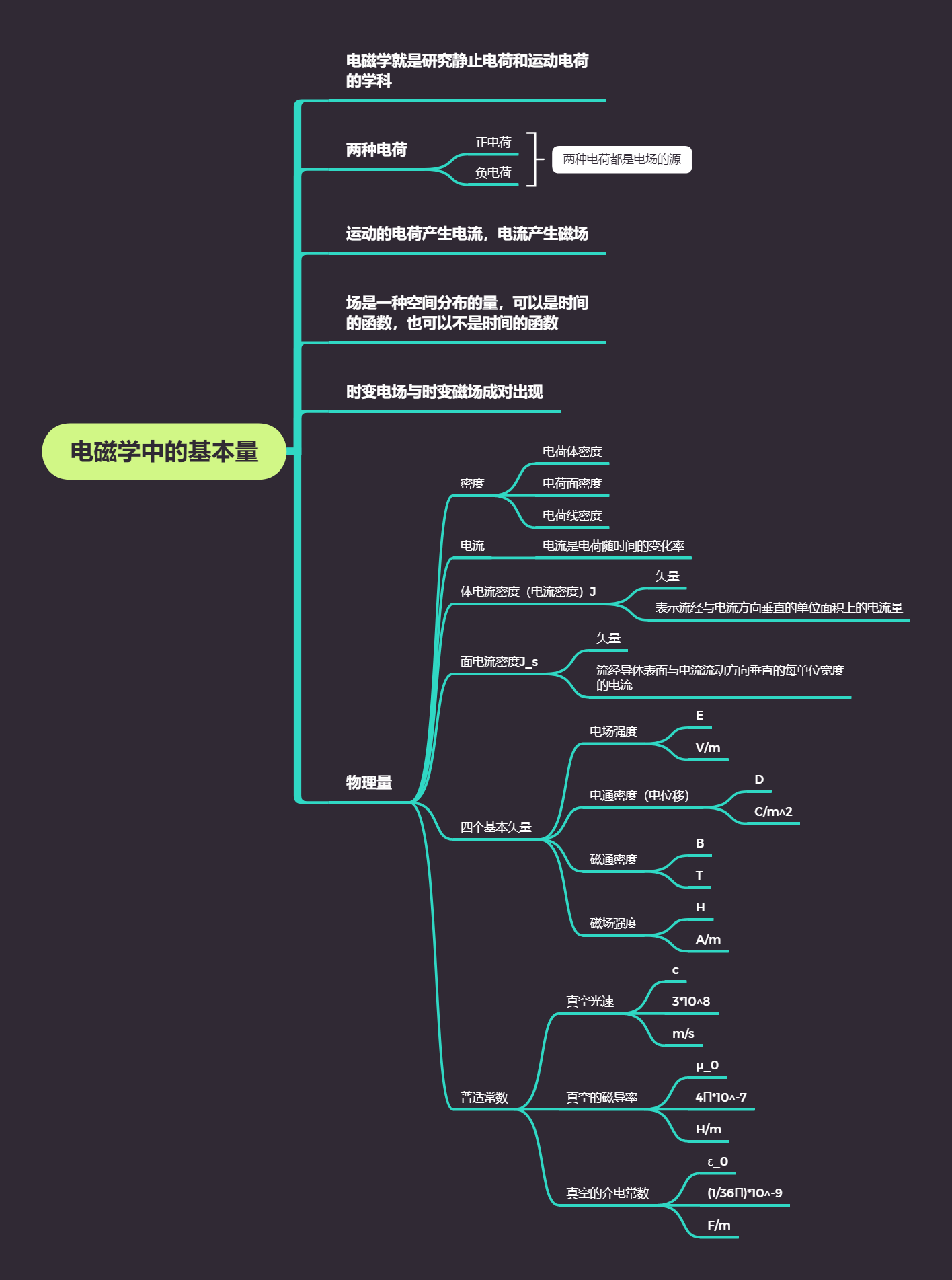
正交坐标系
直角坐标系

圆柱坐标系

球坐标系

坐标转换

矢量分析的数学基础
矢量场的散度唯一地确定场中任一点的通量源强度;
场的旋度唯一地确定场中任一点的旋涡源强度.
从分量式上可以看出,散度取决于场分量的纵向变化率,
而旋度取决于场的横向变化率;
因而,散度和旋度完整地描述了场的分布特性。
1 | |
标量场的等值面

§1.0 哈密顿算子
哈密顿算子定义
性质:矢量性/微分性




三种坐标系下散度计算公式

三种坐标系下旋度计算公式

含两点间距离的微分关系式

§1.1 方向导数与梯度
方向导数定义—标量



梯度定义—矢量
标量场中某点梯度的大小为该点最大的方向导数, 其方向为该点所在等值面的法线方向。
梯度的方向就是等值面的法线方向


梯度的运算规则

§1.2 通量与散度
矢线(场线):在矢量场中,若一条曲线上每一点的切线方向与 场矢量在该点的方向重合,则该曲线称为矢线。
通量定义—标量
通量:如果在该矢量场中取一曲面S, 通过该曲面的矢线量称为通量。



散度定义—标量
通量反映了封闭面中源的总特性,但没有反映源的分布特性; 若要进一步描述源的分布特性,则要引入散度;

用哈密顿算子表示散度

散度的物理意义
散度是 矢量A 通过某点处单位体积的通量 (通量体密度);
它反映了 矢量A 在该点的通量源强度;

散度的运算规则

散度定理
矢量场的散度代表其通量的体密度,因此从散度的定义出 发,散度的体积分等于穿过包围该体积封闭面的总通量


§1.3 环量与旋度
不是所有的矢量场都由通量源激发。存在另一类不同于通量源的矢量源,它所激发的矢量场的力线是闭合的,它对于任何闭合曲面的通量为零。但在场所定义的空间中闭合路径的积分不为零。
环量定义—标量

环量密度—标量


旋度定义—矢量
矢量场的环流给出了矢量场与积分回路所围曲面内旋涡源 宏观联系。
为了给出空间任意点矢量场与旋涡源的关系,引入 矢量场的旋度。

旋度的物理意义

旋度的计算式

哈密顿算子表示旋度


旋度的运算规则

静电场的是无旋场
静止点电荷产生的电场的旋度为0

§1.4 斯托克斯定理
定义

物理意义
一个矢量场旋度的面积分等于该矢量沿此曲面周界的曲 线积分。
斯托克斯定理是闭合曲线积分与曲面积分之间的一个 变换关系式,在电磁理论中也有广泛的应用。
§1.5 Green定理
两大定理

Green定理的应用
将体积V中场的求解问题变换为边界S上场的求解问题。
已知其中一个场的分布,就可以用Green定理求解另一 场的分布特性。
§1.6 场论重要公式
两个重要恒等式
梯无旋
旋无散

三个坐标系下的拉普拉斯算子


常用的矢量恒等式

§1.7 亥姆霍兹定理

矢量场的惟一性定理
位于某一区域中的矢量场,当其散度、旋度以及边界 上场量的切向分量或法向分量给定后,则该区域中的矢 量场被惟一地确定。
已知散度和旋度代表产生矢量场的源,可见惟一性定 理表明,矢量场被其源及边界条件共同决定的。
§1.8 矢量场按源分类
无旋场

无散场

无旋,无散场

有旋,有散场

第二章 电磁场基本方程
1 | |

§2.0 电荷、电流,电荷守恒定理
电荷是产生电场的源
电流是产生磁场的源

§2.1 静态电磁场的基本定律和基本场矢量
1 | |
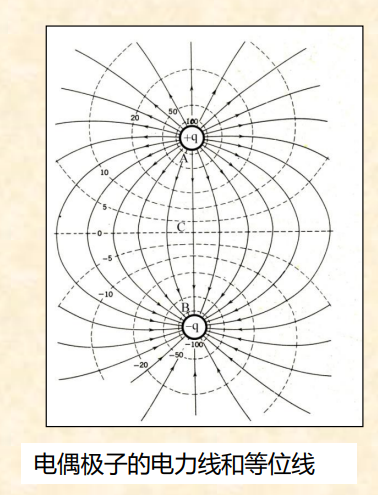
库伦定律

电场强度
源点:场源所在位置
场点:场中任意空间位置

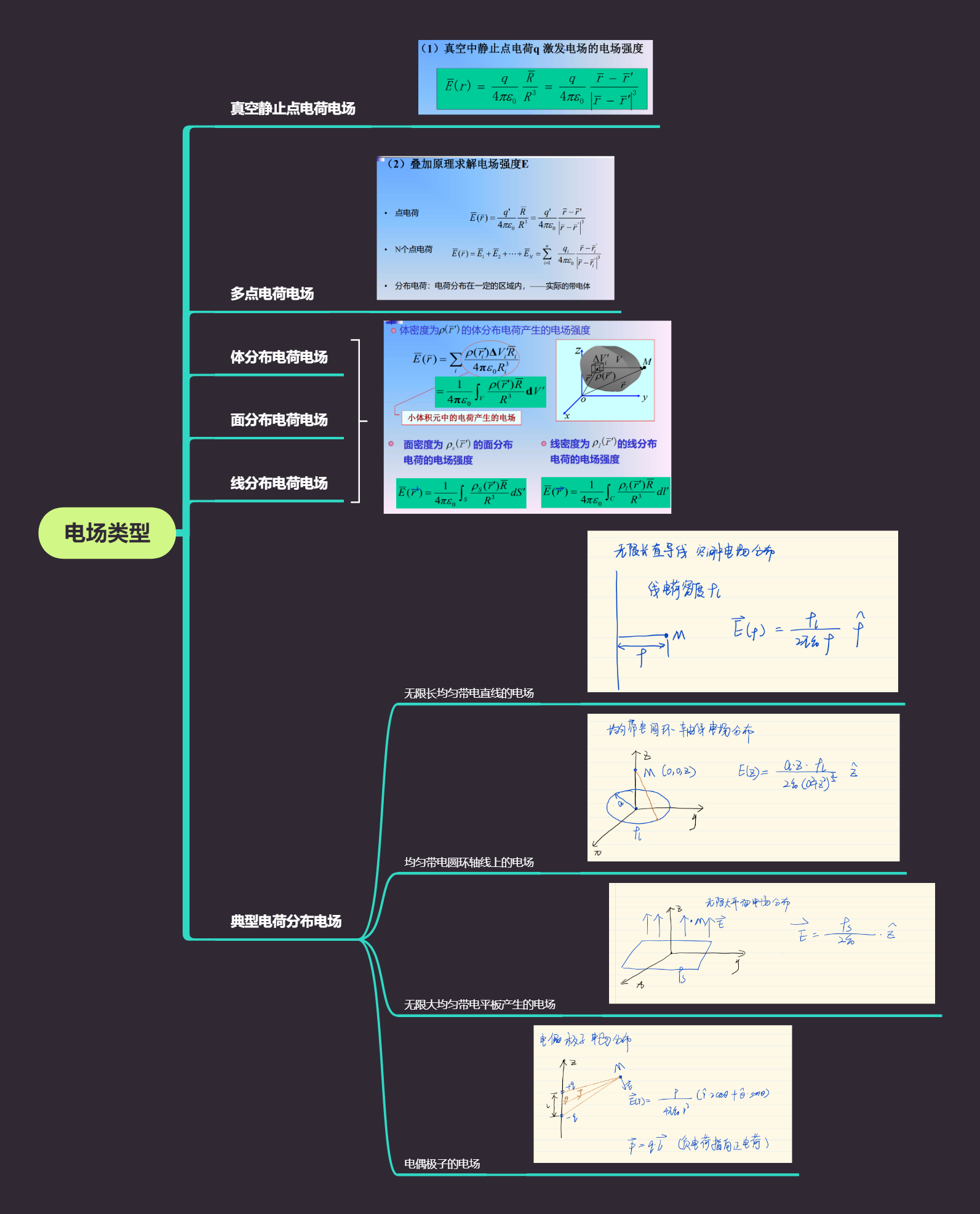
真空中的高斯定理

电场强度的散度

电通密度

介质中的高斯定理

电通密度的散度

静电场常见问题

安培力定律
电流相互作用 力公式,称为安培力定律

毕奥萨法尔定律
电流在其周围空间中产生磁场,描述磁场分布的基本物理量是磁通密度 B(矢量) ,单位为T(特斯拉)。
磁场的重要特征是对场中的电流磁场力作用,载流回路C_1对载流回路 C_2 的作用力是回路 C_1中的电流 I_1产生的磁场对回路 C_2中的电流 I_2的作用力。

磁感应强度/磁通密度
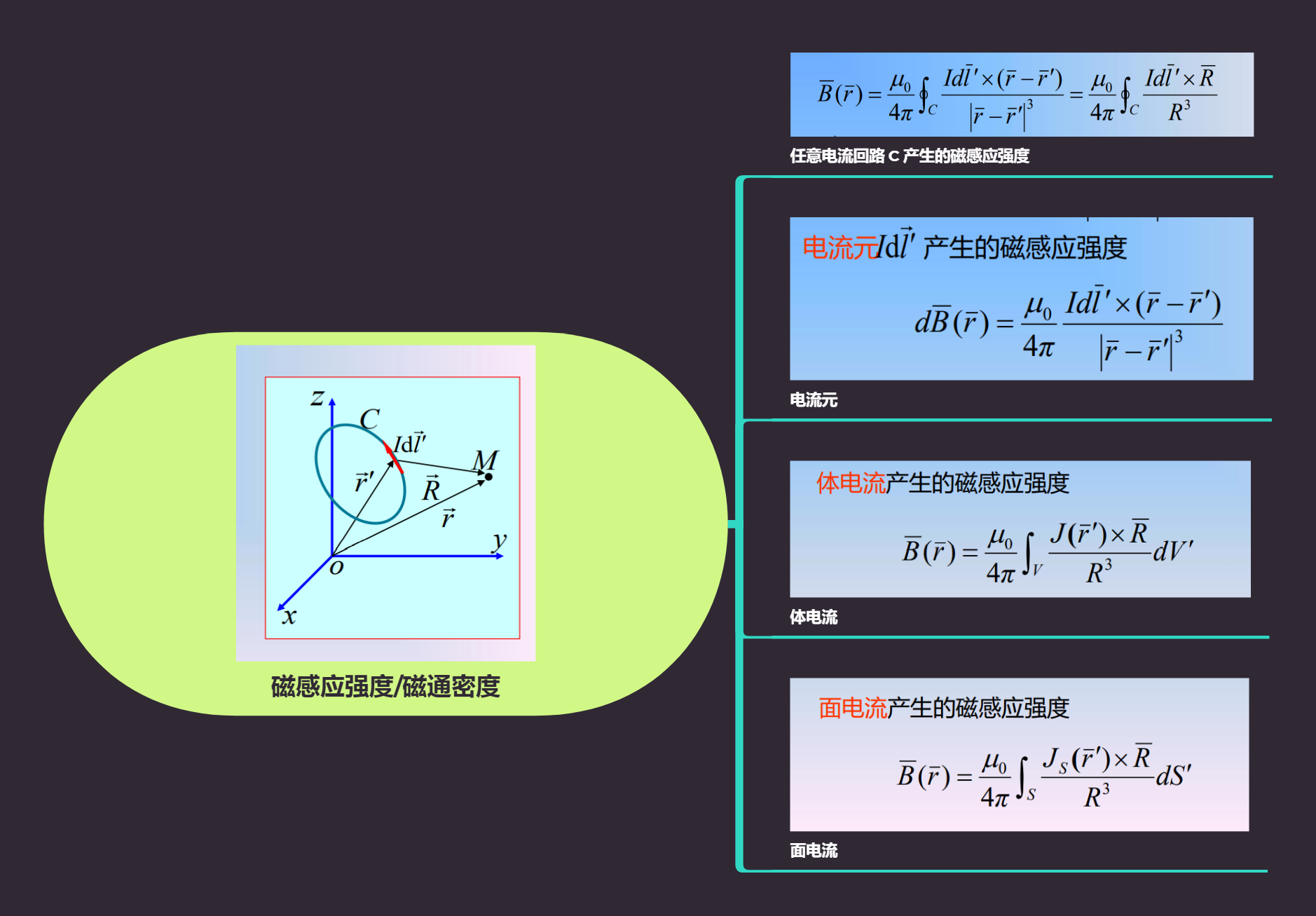


磁通连续性原理
因为自然界中并不存在任何单独的磁荷, 磁力线总是闭合的。

磁场强度

安培环路定理



小结


§2.2 法拉第电磁感应定律和全电流定律
1 | |
法拉第电磁感定律


引起回路中磁通变化的几种情况


位移电流于位移电流密度



全电流连续性原理



传导电流与位移电流对比


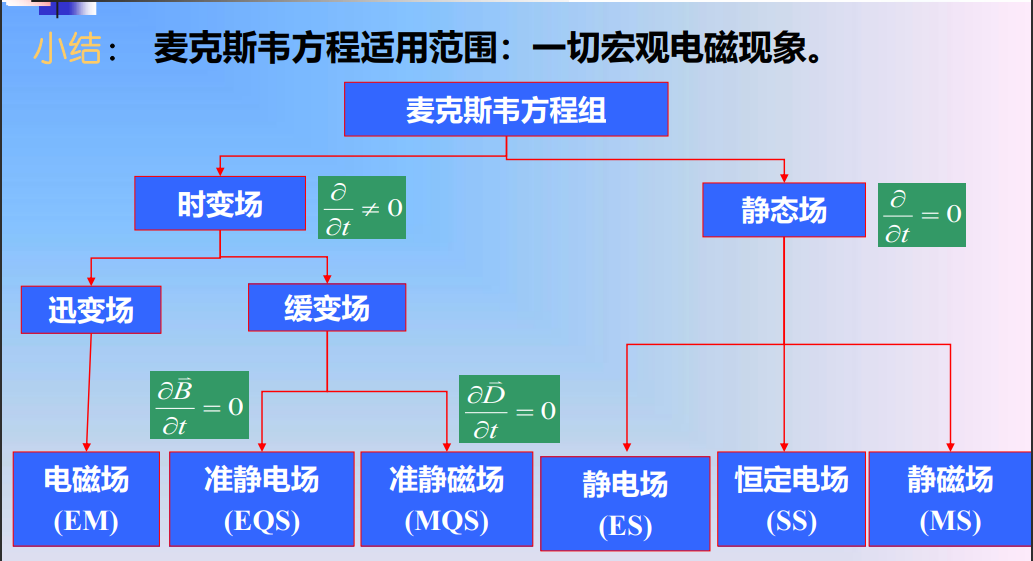
§2.3 麦克斯韦方程组⭐


全电流定律:磁场强度沿任意闭合曲线的环量,等于穿过以闭合曲线为周界的任意曲面的传导电流和位移电流之和;
电磁感应定律:电场强度沿任意闭合曲线的环量,等于穿过以闭合曲线为边界的任意曲面磁通量变化率的负值;
磁通连续性原理:穿过任意闭合曲面的磁感应强度的通量为0;
高斯定理:穿过任意闭合曲面的电位移的通量等于该闭合曲面所包围的自由电荷的代数和;


- 时变电场的激发源除了电荷以外,还有变化的磁场;而时变 磁场的激发源除了传导电流以外,还有变化的电场。电场和 磁场互为激发源,相互激发。
- 时变电磁场的电场和磁场不再相互独立,而是相互关联, 构成一个整体 —— 电磁场。电场和磁场分别是电磁场的两 个分量。
- 在离开辐射源(如天线)的无源空间中,电荷密度和电流密 度矢量为零,电场和磁场仍然可以相互激发,从而在空间形 成电磁振荡并传播,这就是电磁波。
本构关系
在有介质存在时,电场强度矢量和磁感应强度矢量 都与介质的特性有关,因此上述麦克斯韦方程组是不完 备的,还需要再补充描述介质性质的方程:

波动方程


电磁场的位函数——洛伦兹规范
矢量位函数

标量位函数

位函数的非齐次波动方程


泊松方程

§2.4 电磁场的边界条件
• 不同媒质的介电常数ε、磁导率μ、电导率σ不同,在分界面两侧的媒质参数有突变。
• 边界上Maxwell方程组的微分失去意义
• 从积分形式的Maxwell方程组出发推导边界两侧电磁场间的关系。
1 | |
边界条件的一般表达式

电场和磁场切向和法向边界条件

常见情形
两种理想介质间的边界条件

理想介质与理想导体间的边界条件

§2.5 坡印廷定理和坡印廷矢量
1 | |

坡印廷定理—-表征电磁能量守恒关系的定理


坡印廷矢量(电磁能流密度矢量)

场与路的一些对应关系

§2.6 惟一性定理

总结
第三章 静电场及其边值问题的解法

静态场中的电场和磁场是彼此独立存在的。
静电场:第三章
恒定电场:第四章
恒定磁场:第四章

1 | |
§3.1 静电场基本方程与电位方程
静电场的麦克斯韦方程组

静电场的无旋性
静电场中电场力作的功与路径无关, 只取决于始点和终点的位置;
静电场是保守场, 也称位场;
电位
电位参考点

四种分布的电位表达式

电位差U

电位方程——泊松方程与拉普拉斯方程


电位的计算

§3.2 静电场中的介质


介质极化


极化强度


这类介质的极化强度与合成的电场强度的方向相同。 极化强度的某一坐标分量仅决定于相应的电场强度的坐标分量。 极化率与电场方向无关,这类介质称为各向同性介质。
介质的极化率与电场强度的方向有关,也就是极化特性与 电场强度方向有关,因此,这类介质称为各向异性介质。

极化强度矢量与束缚电荷密度


高斯通量定理
真空高斯定理

介质高斯定理
介质中的电通量密度(电位移矢量)的定义!!!



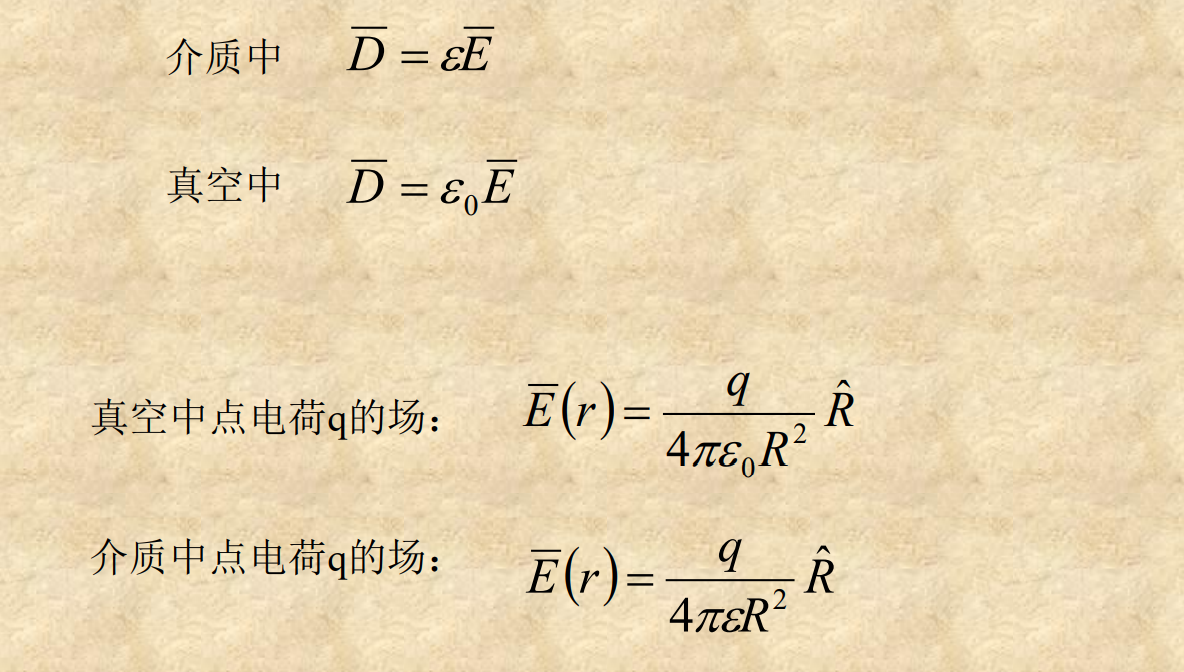
介质中高斯定理的应用


小结
电磁场的基本方程与本构关系

场量

静电场中的两类基本问题

§3.3 静电场中的导体和电容
静电场中的导体——静电平衡


电容
电容的决定式

电容的定义式:C=Q/U




1 | |

1 | |

电容计算的两种方法


§3.4 静电场的边界条件
转2.4 电磁场的边界条件
场量的边界条件



两种特殊的电场边界条件
介质与导体间边界条件

两种介质间边界条件


电位φ满足的边界条件



介质与导体间的电位边界条件

介质与介质之间的电位边界条件

边界条件的重要性 1. 构成边值问题必不可少的条件; 2. 判断不同媒质界面两侧场量的大小、方向及连续、突变
§3.5 静电场边值问题,惟一性定理
1 | |

静电场边值问题及其分类



边值问题的解法

唯一性定理

§3.6 镜像法
1 | |
镜像法的基本原理
非均匀感应电荷产生的电位很难求 解,可以用等效电荷的电位替代
所谓镜像法是将不均匀电荷分布的作用等效为点电荷 或线电荷的作用。



接地导体平面的镜像
点电荷对无限大接地导体平面的镜像



线电荷对无限大接地导体平面的镜像

点电荷对半无限大接地导体角域 (导体劈) 的镜像




点电荷对无限大介质平面的镜像



导体球面的镜像
接地导体球



导体球不接地、不带电荷

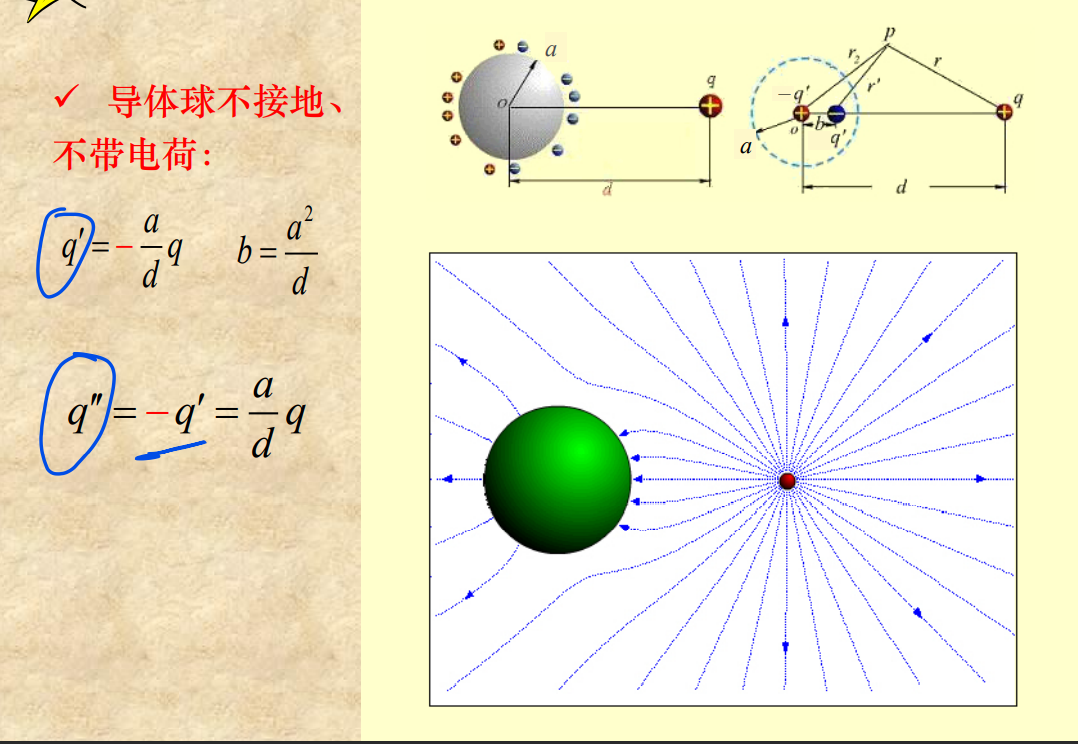
导体球不接地、带电荷

接地导体球壳


导体圆柱面的镜像ppt 159
线电荷对接地导体圆柱面的镜像
平行圆柱导体的电轴
半径不同的两平行圆柱导体问题
线电流对无限大磁介质平面的镜像(矢量位)
线电流对无限大磁介质平面的镜像(磁场强度)
镜像法 小结


§3.7 分离变量法

0.双曲函数


1 | |
1. 分离变量法解题的基本步骤

2. 直角坐标系中的分离变量法
二维拉普拉斯方程





三维拉普拉斯方程


3. 圆柱坐标系中的分离变量法

4. 球坐标系中的分离变量法

5. 复变函数法

第四章 恒定电场和恒定磁场
1 | |
§4.1 恒定电场
1. 恒定电场的基本方程 ⭐


2. 恒定电场的边界条件




3. 静电比拟法



§4.2 恒定磁场的基本方程和边界条件


§4.3 恒定磁场的矢量磁位



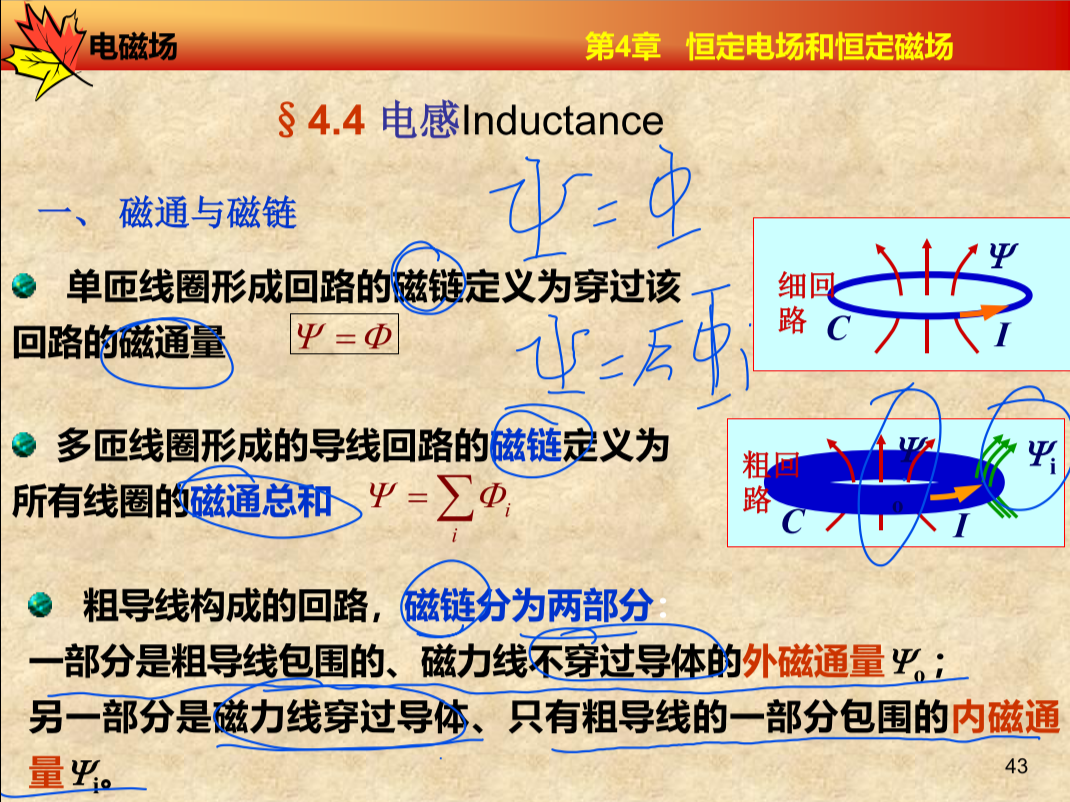
§4.4 电感Inductance





第五章 时变电磁场和平面电磁波
§5.1 时谐电磁场的复数表示



§5.2 复数形式Maxwell方程组




§5.3 复坡印廷矢量和复坡印廷定理
电磁场是具有能量的,时谐电磁场的能量在空间以电磁波形式传播
Poynting定理是时变电磁场中能量守恒定律的表达形式


§5.4 理想介质中的平面波

均匀平面波满足一维波动方程


均匀平面波是横电磁波(TEM波)



波动方程的解

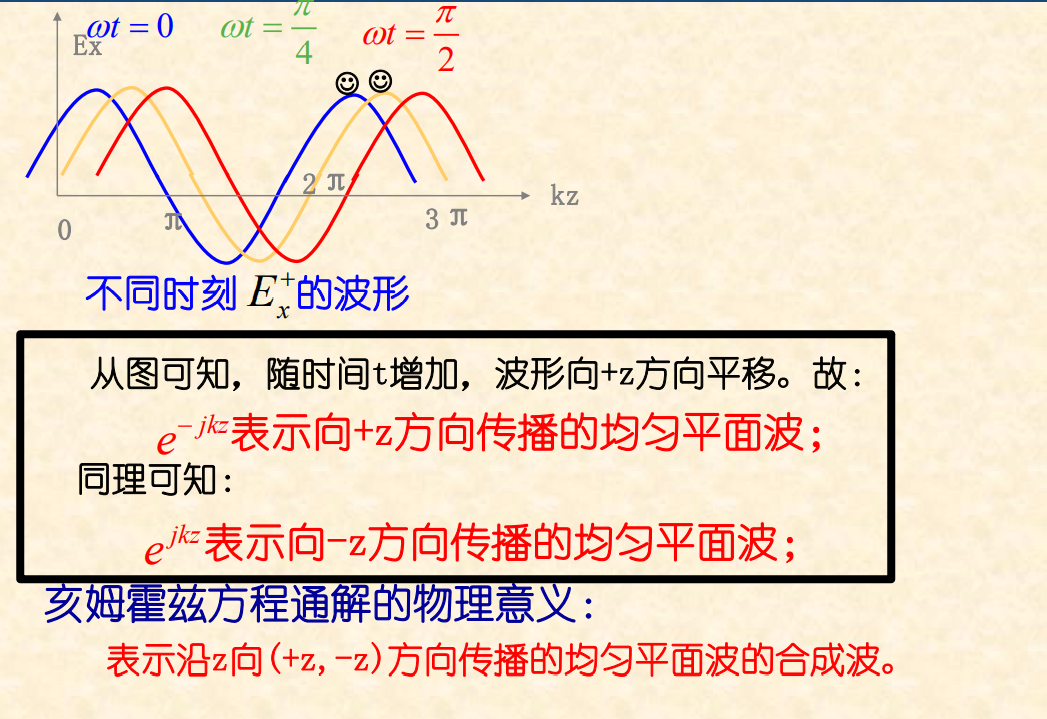
相位常数k


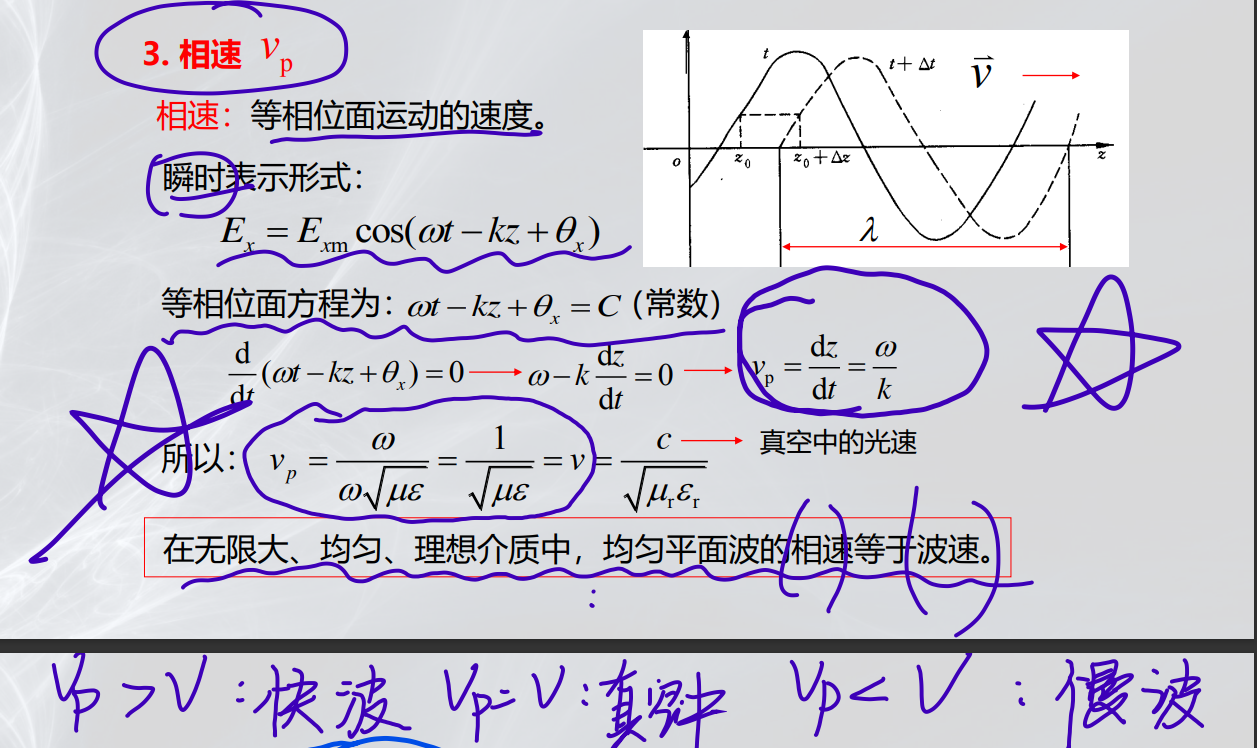
相速 v
介质的本质阻抗 η

§5.5 导电介质中的平面波


复介电常数和复本质阻抗

相位常数和衰减系数

相速和色散现象

有耗媒质中电磁场表示


有耗媒质中的坡印廷矢量

趋肤效应和趋肤深度





§5.7 电磁波的极化

极化的概念



线极化波

圆极化波



椭圆极化波


极化波的分解
极化波的工程应用

第六章 平面电磁波的反射和折射

平面波在边界上的反射及透射规律与媒质特性及边界形状有关。
仅讨论平面波在无限大的平面边界上的反射及透射特性
§6.1 平面波对平面边界的垂直入射
入射波 (Incident Wave)
反射波 (Reflected Wave) —- 一部分能量被反射回来形成
透射波 (Transmitted Wave) —- 另一部分能量穿过边界形成
反射波与折射波的特性由分界面两侧媒质的参数确定。
• 对理想导体的垂直入射





驻波


•空间各点的电场都随时间t按正弦规律变化,但是波腹和波节点的位置均固定不变。
•这种波与行波不同,它是驻立不动的,称之为驻波。
•驻波就是波腹点和波节点固定不动的电磁波。
磁场的波腹点是电场的波节点, 磁场的波节点是电场的波腹点。
面电流

功率流密度



当均匀平面波垂直入射到理想导体表面时,在表面上发生全 反射,反射波与入射波的迭加在自由空间中形成驻波。
在理想导体表面上,电场为零,磁场为最大值。


YXR——PPT 6.1 P27例题 P31例题
• 对理想介质的垂直入射







入射波能量、反射波能量和透射波能量间的关系——坡印廷矢量平均值


区域1中传输的合成场功率等于向区域2透射的功率
YXR_PPT_P53——例题
• 对多层边界的垂直入射
PPT 58页
§6.2 平面波对平面边界的斜入射
斜入射的概念





垂直极化波的斜入射




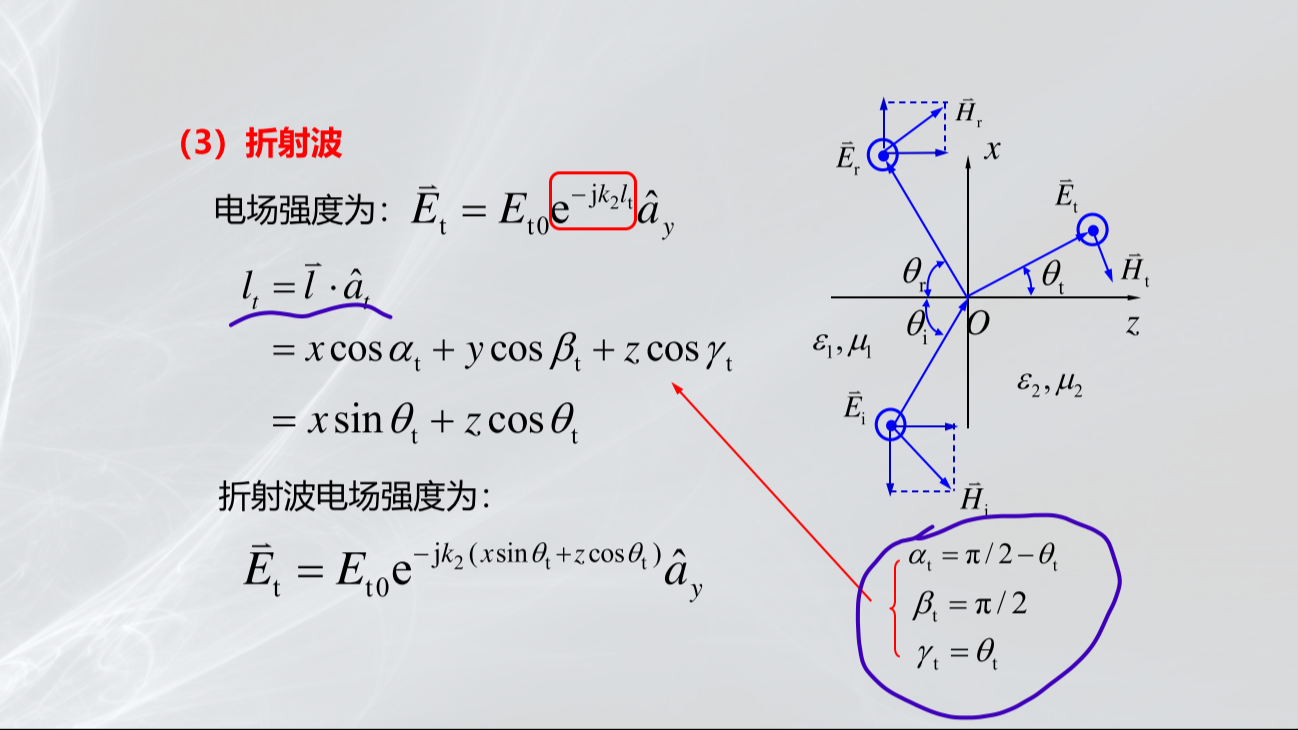







平行极化波的斜入射



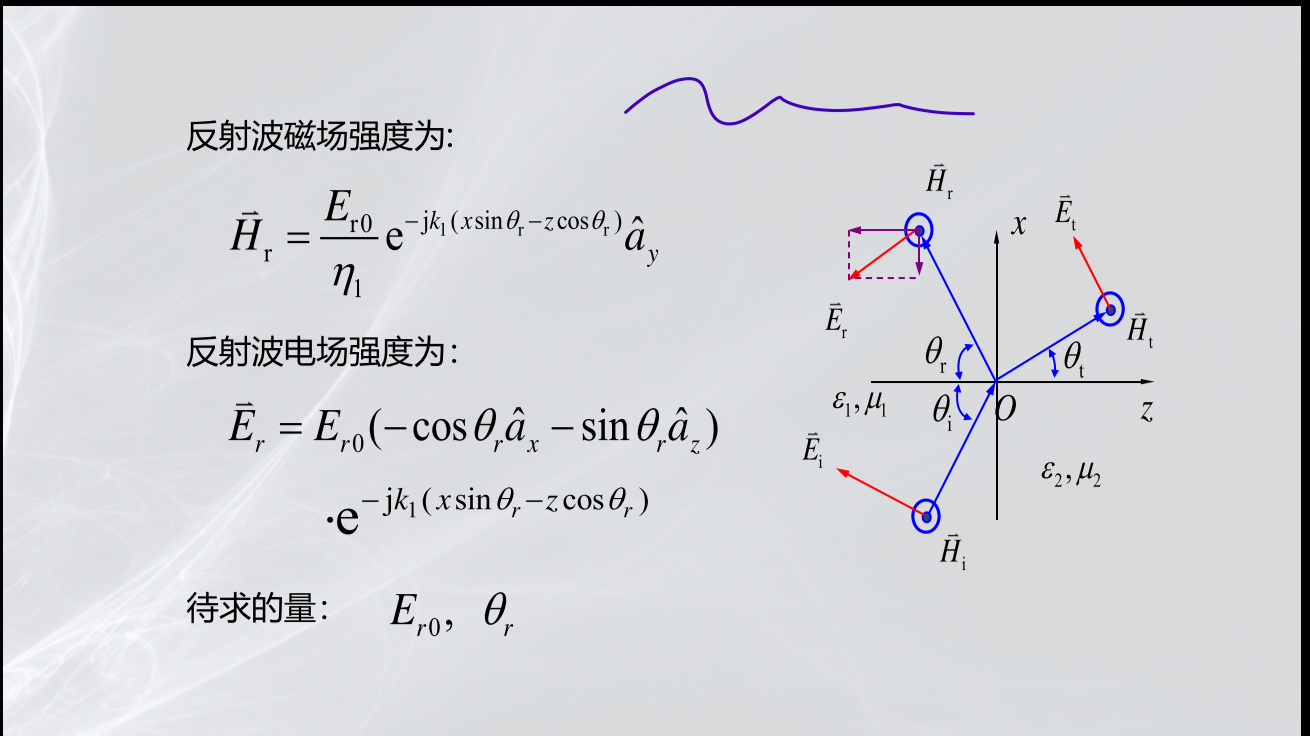




§6.3 全反射 全折射
全反射



全折射



