动手学深度学习v2

李沐简介

李沐于2004年进入上海交通大学计算机科学与工程系进行本科学习；2009年至2010年担任香港科技大学研究助理；2011年至2012年担任百度高级研究员；2012年至2017年在美国卡内基梅隆大学攻读博士学位。2019年编著的《动手学深度学习》出版。

李沐是深度学习框架MXNet的作者之一。他先后担任过机器学习创业公司Marianas Labs的CTO和百度深度学习研究院的主任研发架构师。他在理论、机器学习、应用和操作系统等多个领域的顶级学术会议（包括FOCS、ICML、NeurIPS、AISTATS、CVPR、KDD 、WSDM、OSDI）上发表过论文。

https://www.linkedin.com/in/mulicmu?trk=people-guest_people_search-card

深度学习环境配置本地

有了第一次配置深度学习痛苦的经历，第二次完全是轻车熟路！

CUDA 112 + cuDNN 8.1
Miniconda3-py38-4.9.2
PyTorch
TensorFlow

2022年3月，尝试跟着李沐老师一起学习，但课程任务比较重，最后还是放弃了！

云服务器D2L运行

2022年9月，保研前后的这段时间，我再一次准备跟上李沐老师的步伐！

在云服务器上将D2L跑起来了，跟着李沐老师一步步学习了！
有一点遗憾是云服务器上没有GPU，且CPU性能也很一般，前期其实也用不到GPU，先跟着做吧！能不在本地做，就不在本地做了，上云是最好的了！但是GPU服务器太贵了，以后看看白嫖Google Colab吧！

课程安排 - 动手学深度学习课程 (d2l.ai)

动手学深度学习 2.0.0-beta1 documentation (d2l.ai)

应用深度学习需要同时理解：

问题的动机和特点；

将大量不同类型神经网络层通过特定方式组合在一起的模型背后的数学原理；

在原始数据上拟合极复杂是深层次模型的优化算法；

有效训练模型、避免数值计算陷阱以及充分利用计算机硬件性能所需的工程技能；

为解决方案挑选合适的变量（超参数）组合的经验。

这次学到了Softmax这里，但是由于没有机器学习的基础，我已经听不懂了，就转向了吴恩达的机器学习！

D2L，这次我要坚持到底

2022年11月，学习完吴恩达老师的机器学习之后，我意见学习了很多机器学习的基础知识了，我再次回到了这里，这次，我要坚持到底！！！

参考资料：

视频课程：跟李沐学AI的个人空间_哔哩哔哩_bilibili
- 00 预告【动手学深度学习v2】_哔哩哔哩_bilibili
- 课程安排 - 动手学深度学习课程 (d2l.ai)
电子书（第二版）：MXNet、PyTorch、TensorFlow
- 序言 — 动手学深度学习 2.0.0-beta1 documentation (d2l.ai)
- Preface — Dive into Deep Learning 1.0.0-alpha1.post0 documentation (d2l.ai)
纸质书（第一版）：MXNet
- 《动手学深度学习》动手学深度学习 (豆瓣) (douban.com)

因为感觉听课其实学的很迷糊，还是以纸质书和电子书为主，以视频为辅吧！

环境配置问题

jupyter notebook切换虚拟环境

jupyter notebook怎么切换到特定的anaconda虚拟环境_Yee_Ko的博客-CSDN博客
 在anaconda中新建环境，并在jupyter notebook添加kernel_小xiao露的博客-CSDN博客_anaconda 新建的虚拟环境中在jupyter notebook 只有一个kernel

第一步：创建一个新的虚拟环境，这里我电脑已经有了一个装有torch的环境AAA，为了不污染这个环境，我直接复制AAA环境中的包到环境BBB中：conda create -n BBB --clone AAA
第二步：在虚拟环境下创建kernel：conda install -n BBB ipykernel
第三步：激活虚拟环境：source activate BBB
第四步：将该虚拟环境写进notebook的kernel中：python -m ipykernel install --user --name BBB --display-name "python deep_pytorch"
这时你在base环境中输入jupyter notebook打开notebook，点击右上角的”new”，这时“notebook:”列表下便会显示两个kerbel名称了。（这里要注意只能在base环境中打开jupyter notebook，因为只有base环境中装了它，虚拟环境中并没有装，而只是装了它的kernel）
还有一个tip是如果在代码编辑界面想要更改kernel，直接点击菜单栏的“Kernel”，接着点击”change kernel”，选择你想要的kernel即可。

(d2l-zh) ubuntu@VM-8-15-ubuntu:~/userDoc/limu-d2l$ pip install ipykernel

(d2l-zh) ubuntu@VM-8-15-ubuntu:~/userDoc/limu-d2l$ python -m ipykernel install --user --name d2l-zh --display-name "D2L-ZH"
Installed kernelspec d2l-zh in /home/ubuntu/.local/share/jupyter/kernels/d2l-zh

以下章节划分均按照《动手学深度学习》电子书

附录A 数学基础

先把需要用到的数学知识学一下吧

线性代数：向量，矩阵，运算方式，范数，特征值与特征向量
微分：导数和微分，泰勒展开，偏导数，梯度，海森矩阵
概率：条件概率，期望，均匀分布

–

附录B Jupyter Notebook使用方法

JupyterNotebook | Murphy’s Blog (cosmicdusty.cc)

–

第一部分深度学习基础

第一章前言

赫布理论

赫布理论 - 维基百科，自由的百科全书 (wikipedia.org)
赫布理论（英语：Hebbian theory）是一个神经科学理论，解释了在学习的过程中脑中的神经元所发生的变化。赫布理论描述了突触可塑性的基本原理，即突触前神经元向突触后神经元的持续重复的刺激，可以导致突触传递效能的增加。
强化合意的行为、惩罚不合意的行为，最终获得优良的神经网络参数。
神经网络包含的核心原则：
- 　交替使用线性处理单元和非线性处理单元，它们通常被称为“层”；
- 　使用链式法则（即反向传播）来更新网络的参数。
Iris
- UCI Machine Learning Repository: Iris Data Set
MNIST
机器学习与深度学习的关系
- _机器学习_（machine learning，ML）是一类强大的可以从经验中学习的技术。通常采用观测数据或与环境交互的形式，机器学习算法会积累更多的经验，其性能也会逐步提高。
- 机器学习研究如何使计算机系统利用经验改善性能。它是人工智能领域的分支，也是实现人工智能的一种手段。
- 在机器学习的众多研究方向中，表征学习关注如何自动找出表示数据的合适方式，以便更好地将输入变换为正确的输出。
- 深度学习是具有多级表示的表征学习方法。在每一级（从原始数据开始），深度学习通过简单的函数将该级的表示变换成更高级的表示。
- 因此深度学习模型也可以看作是由许多简单函数复合而成的函数。当这些复合的函数足够多时，深度学习模型就可以表达非常复杂的变换。
- 深度学习可以逐级表示越来越抽象的概念或模式。深度学习将自动找出每一级表示数据的合适方式。
- 端到端的训练：将整个系统组建好之后一起训练，而不是单端调试每一部分最后再拼起来。
- 从含参数统计模型转向完全无参数的模型。

你可以把参数看作是旋钮，我们可以转动旋钮来调整程序的行为。任一调整参数后的程序，我们称为模型（model）。通过操作参数而生成的所有不同程序（输入-输出映射）的集合称为“模型族”。使用数据集来选择参数的元程序被称为学习算法（learning algorithm）。

在机器学习中，学习（learning）是一个训练模型的过程。通过这个过程，我们可以发现正确的参数集，从而使模型强制执行所需的行为。换句话说，我们用数据训练（train）我们的模型。
训练过程通常包含如下步骤：

从一个随机初始化参数的模型开始，这个模型基本毫不“智能”。

获取一些数据样本（例如，音频片段以及对应的是否{是,否}标签）。

调整参数，使模型在这些样本中表现得更好。

重复第2步和第3步，直到模型在任务中的表现令你满意。

机器学习问题中的关键组件：
1. 我们可以学习的数据（data）。
2. 如何转换数据的模型（model）。
3. 一个目标函数（objective function），用来量化模型的有效性。在机器学习中，我们需要定义模型的优劣程度的度量，这个度量在大多数情况是“可优化”的，我们称之为目标函数（objective function）。我们通常定义一个目标函数，并希望优化它到最低点。因为越低越好，所以这些函数有时被称为损失函数（loss function，或cost function）。
4. 调整模型参数以优化目标函数的算法（algorithm）。
  - 一旦我们获得了一些数据源及其表示、一个模型和一个合适的损失函数，我们接下来就需要一种算法，它能够搜索出最佳参数，以最小化损失函数。深度学习中，大多流行的优化算法通常基于一种基本方法–梯度下降（gradient descent）。
监督学习（supervised learning）
- 回归（regression）
- 分类（classification）
- 多标签分类（multi-label classification）
- 搜索
- 推荐系统（recommender system）
- 序列学习：标记和解析，自动语音识别，文本到语音，机器翻译
无监督学习（unsupervised learning）
- 聚类（clustering）问题
- 主成分分析（principal component analysis）问题
- 因果关系（causality）和_概率图模型_（probabilistic graphical models）问题
- 生成对抗性网络（generative adversarial networks）
与环境互动
- 离线学习（offline learning）：监督学习和无监督学习，预先获取大量的数据，启动模型，与环境不再交互。
强化学习（reinforcement learning）
- 深度强化学习（deep reinforcement learning）将深度学习应用于强化学习的问题，是非常热门的研究领域。
- 突破性的深度Q网络（Q-network）在雅达利游戏中仅使用视觉输入就击败了人类，以及 AlphaGo 程序在棋盘游戏围棋中击败了世界冠军，是两个突出强化学习的例子。
- 强化学习的目标是产生一个好的策略（policy）。
- 我们可以将任何监督学习问题转化为强化学习问题。
- 强化学习者必须处理学分分配（credit assignment）问题：决定哪些行为是值得奖励的，哪些行为是需要惩罚的。
- 当环境可被完全观察到时，我们将强化学习问题称为马尔可夫决策过程（markov decision process）。当状态不依赖于之前的操作时，我们称该问题为上下文赌博机（contextual bandit problem）。当没有状态，只有一组最初未知回报的可用动作时，这个问题就是经典的多臂赌博机（multi-armed bandit problem）。

第二章预备知识

2.1 数据操作
n维数组，也称为张量（tensor），无论使用哪个深度学习框架，它的_张量类_（在MXNet中为ndarray，在PyTorch和TensorFlow中为Tensor）都与Numpy的ndarray类似。但深度学习框架又比NumPy的ndarray多一些重要功能：GPU很好地支持加速计算，而NumPy仅支持CPU计算；其次，张量类支持自动微分。这些功能使得张量类更适合深度学习。

张量连结（concatenate）
- 张量与张量端对端地叠起来形成一个更大的张量
- dim=0：在行上
- dim=1：在列上
广播机制
- 对于不同形状的两个张量如何运算？
- 首先，通过适当复制元素来扩展一个或两个数组，以便在转换之后，两个张量具有相同的形状。其次，对生成的数组执行按元素操作。
- 张量的广播机制_luoganttcc的博客-CSDN博客_张量广播
  - 如果两个数组的后缘维度(从末尾开始算起的维度)的轴长度相符或其中一方的长度为1，则认为它们是广播兼容的。广播会在缺失维度和(或)轴长度为1的维度上进行。
  - pytorch笔记：张量的广播机制 | 高深远的博客 (gsy00517.github.io)
  - Broadcasting semantics — PyTorch 1.13 documentation
    - Two tensors are “broadcastable” if the following rules hold:
      - Each tensor has at least one dimension.
      - When iterating over the dimension sizes, starting at the trailing dimension, the dimension sizes must either be equal, one of them is 1, or one of them does not exist.
    - 当一对张量满足下面的条件时，它们才是可以被“广播”的。
      - 1.每个张量至少有一个维度。
      - 2.迭代维度尺寸时，从尾部（也就是从后往前）开始，依次每个维度的尺寸必须满足以下之一：
        
        相等。
        
        其中一个张量的维度尺寸为1。
        
        其中一个张量不存在这个维度。
节省内存
- 我们希望原地执行这些更新。
- Z[:] = X + Y
- X += Y

2.2 数据预处理

pandas
Pandas loc/iloc用法详解 (biancheng.net)

2.3 线性代数

向量或轴的维度被用来表示向量或轴的长度，即向量或轴的元素数量。然而，张量的维度用来表示张量具有的轴数。
张量解释——深度学习的数据结构 (qq.com)
深度学习中关于张量的阶、轴和形状的解释 | Pytorch系列（二） (qq.com)
张量简介 | TensorFlow Core (google.cn)
降维
- 默认情况下，调用求和函数会沿所有的轴降低张量的维度，使它变为一个标量。
- 我们还可以[指定张量沿哪一个轴来通过求和降低维度]。以矩阵为例，为了通过求和所有行的元素来降维（轴0），我们可以在调用函数时指定axis=0。由于输入矩阵沿0轴降维以生成输出向量，因此输入轴0的维数在输出形状中消失。
计算
- torch.dot(vector_a, vector_b)
- torch.mv(matrix_a, vertor_b)
- torch.mm(matrix_A, matrix_B)
范数（norm）
- 非正式地说，一个向量的范数告诉我们一个向量有多大。这里考虑的大小（size）概念不涉及维度，而是分量的大小。
- 在线性代数中，向量范数是将向量映射到标量的函数$f$。
- 欧几里得距离是一个$L_2$范数
- $L_2$范数:torch.norm(x)
- $L_1$范数:torch.abs(x).sum()
标量、向量、矩阵和张量分别具有零、一、二和任意数量的轴。
torch.linalg.norm — PyTorch 1.13 documentation

2.4 微积分

我们可以将拟合模型的任务分解为两个关键问题：
- 优化（optimization）：用模型拟合观测数据的过程；
- 泛化（generalization）：数学原理和实践者的智慧，能够指导我们生成出有效性超出用于训练的数据集本身的模型。

2.5 自动微分

深度学习框架通过自动计算导数，即 自动微分 （automatic differentiation）来加快求导。实际中，根据我们设计的模型，系统会构建一个 计算图 （computational graph），来跟踪计算是哪些数据通过哪些操作组合起来产生输出。自动微分使系统能够随后反向传播梯度。这里，反向传播（backpropagate）意味着跟踪整个计算图，填充关于每个参数的偏导数。

自动求导是计算一个函数在指定值上的导数，这与符号求导和数值求导有区别
- 自动求导：计算函数在指定值上的导数；（PyTorch✔）
- 符号求导：根据函数表达式，计算出导数表达式（数学计算中）；
- 数值求导：给定一个不知道表达式的函数，通过数值拟合出导数。
计算图
- 将代码分解成操作子
- 将计算表示成一个无环图
- 显示构造：TensorFlow/Theano/MXNet
- 隐示构造：PyTorch/MXNet
自动求导有两种模式
- 正向累计
- 反向累计（反向传递）（backpropagate）(✔)

存储梯度

1	`x.requires_grad_(True) # 等价于x=torch.arange(4.0,requires_grad=True)`

清除梯度，防止梯度累加

1 2	`# 在默认情况下，PyTorch会累积梯度，我们需要清除之前的值 x.grad.zero_()`

非标量变量的反向传播 （没听懂）

深度学习中，不是为了计算微分矩阵，而是批量中每个样本单独计算的偏导数之和。

大多数情况下都是对标量进行求导✔

# 对非标量调用backward需要传入一个gradient参数，该参数指定微分函数关于self的梯度。
# 在我们的例子中，我们只想求偏导数的和，所以传递一个1的梯度是合适的
x.grad.zero_()
y = x * x
# 等价于y.backward(torch.ones(len(x)))
y.sum().backward()
x.grad

---
tensor([0., 2., 4., 6.])

深度学习框架可以自动计算导数：我们首先将梯度附加到想要对其计算偏导数的变量上。然后我们记录目标值的计算，执行它的反向传播函数，并访问得到的梯度。

2.6 概率

2.7 查阅文档

1	`help(torch.ones)`

通常，我们可以忽略以“__”（双下划线）开始和结束的函数（它们是Python中的特殊对象），或以单个“_”（单下划线）开始的函数（它们通常是内部函数）。

第三章线性神经网络

3.1 线性回归

training set; sample; label; feature;
线性模型
- _模型参数_（model parameters）𝐰和𝑏
- 需要两个辅助模型的东西：（1）一种模型质量的度量方式；（2）一种能够更新模型以提高模型预测质量的方法。
损失函数
- _损失函数_（loss function）能够量化目标的_实际_值与_预测_值之间的差距。
- 回归问题中最常用的损失函数是平方误差函数。
解析解
- 与我们将在本书中所讲到的其他大部分模型不同，线性回归的解可以用一个公式简单地表达出来，这类解叫作解析解（analytical solution）。
随机梯度下降
- _梯度下降_（gradient descent）
- 梯度下降最简单的用法是计算损失函数（数据集中所有样本的损失均值）关于模型参数的导数（在这里也可以称为梯度）。但实际中的执行可能会 非常慢：因为在每一次更新参数之前，我们必须遍历整个数据集。因此，我们通常会在每次需要计算更新的时候随机抽取一小批样本，这种变体叫做_小批量随机梯度下降_（minibatch stochastic gradient descent）。
- 步骤：（1）初始化模型参数的值，如随机初始化；（2）从数据集中随机抽取小批量样本且在负梯度的方向上更新参数，并不断迭代这一步骤。
超参数
- |B|表示每个小批量中的样本数，这也称为_批量大小_（batch size）。 𝜂表示_学习率_（learning rate）。批量大小和学习率的值通常是手动预先指定，而不是通过模型训练得到的。这些可以调整但不在训练过程中更新的参数称为_超参数_（hyperparameter）。
- _调参_（hyperparameter tuning）是选择超参数的过程。超参数通常是我们根据训练迭代结果来调整的，而训练迭代结果是在独立的_验证数据集_（validation dataset）上评估得到的。
- 超参数 (机器学习) - 维基百科，自由的百科全书 (wikipedia.org)
- Hyperparameter (machine learning) - Wikipedia
- 在机器学习中，超参数(英语：Hyperparameter)是事先给定的，用来控制学习过程的参数。而其他参数（例如节点权重）的值是通过训练得出的。
- 事实上，更难做到的是找到一组参数，这组参数能够在我们从未见过的数据上实现较低的损失，这一挑战被称为_泛化_（generalization）。
给定特征估计目标的过程通常称为_预测_（prediction）或_推断_（inference）。
从线性回归到深度网络
- 线性回归是一个单层神经网络。

3.2 线性回归的从零开始实现

生成器 Generator
- generator - What does the “yield” keyword do in Python? - Stack Overflow
- python中yield的用法详解——最简单，最清晰的解释_冯爽朗的博客-CSDN博客_python yield
定义模型：线性回归模型
定义损失函数：MSE（均值平方误差函数）
定义优化算法：SGD（小批量随机梯度下降）
- with torch.no_grad():【pytorch系列】 with torch.no_grad():用法详解_大黑山修道的博客-CSDN博客_with torch.no_grad()作用
- 在该模块下，所有计算得出的tensor的requires_grad都自动设置为False。
- 当requires_grad设置为False时,反向传播时就不会自动求导了。
训练
- 初始化模型参数
- 重复
  - 计算梯度
  - 更新参数w和b

3.3 线性回归的简洁实现

定义模型

1
2
3

# nn是神经网络的缩写
from torch import nn
net = nn.Sequential(nn.Linear(2, 1))

初始化模型参数

1 2	`net[0].weight.data.normal_(0, 0.01) net[0].bias.data.fill_(0)`

定义损失函数
1
loss = nn.MSELoss()

定义优化算法

1 2	`trainer = torch.optim.SGD(net.parameters(), lr=0.03) # lr : learning rate`

训练
- 通过调用net(X)生成预测并计算损失l（前向传播）。
- 通过进行反向传播来计算梯度。
- 通过调用优化器来更新模型参数。
凹函数和凸函数
- 凸函数与凹函数 - 知乎 (zhihu.com)
- 什么是凹函数和凸函数？（图文举例详细说明） - 荒原之梦 (zhaokaifeng.com)
requires_grad=True
- 自动求导机制 - PyTorch中文文档 (pytorch-cn.readthedocs.io)
Sequential
- PyTorch 中的 ModuleList 和 Sequential: 区别和使用场景 - 知乎 (zhihu.com)
机器学习中大部分都是NP Complete 问题
- NP完全 - 维基百科，自由的百科全书 (wikipedia.org)
- NP-Complete - A Rough Guide (mathsisfun.com)

3.4 softmax 回归

softmax回归是分类问题
回归于分类问题的区别
- 回归：单连续数值输出；分类：通常是多输出
- 回归：跟真实值的区别作为损失；分类：输出i是预测为第i类的置信度。
类别编码
- _独热编码_（one-hot encoding）。独热编码是一个向量，它的分量和类别一样多。类别对应的分量设置为1，其他所有分量设置为0。
似然函数
- 似然函数 - 维基百科，自由的百科全书 (wikipedia.org)
argmax
- 最大值自变量点集
- argmax - 知乎 (zhihu.com)
- Arg max - Wikipedia
- What Is Argmax in Machine Learning? (machinelearningmastery.com)
softmax回归模型
- softmax回归的输出值个数等于标签里的类别数。
- softmax函数能够将未规范化的预测变换为非负数并且总和为1，同时让模型保持可导的性质。
- softmax回归的矢量计算表达式为：
  $$ \begin{aligned} \mathbf{O} &= \mathbf{X} \mathbf{W} + \mathbf{b}, \ \hat{\mathbf{Y}} & = \mathrm{softmax}(\mathbf{O}). \end{aligned} $$
损失函数
- 交叉熵 cross entropy
- 交叉熵损失函数
信息论
- 信息量
- 熵
- 我们可以从两方面来考虑交叉熵分类目标：（i）最大化观测数据的似然；（ii）最小化传达标签所需的惊异。

3.5 图像分类数据集

数据集
- MNIST
  - MNIST database - Wikipedia
  - deepai.org
- ImageNet
  - ImageNet (image-net.org)
- Fashion MNIST
  - Fashion MNIST | Kaggle
  - Fashion-MNIST：替代MNIST手写数字集的图像数据集 - 知乎 (zhihu.com)

3.6 softmax回归的从零开始实现

初始化模型参数
- 输入是图像（28*28 = 784）
- 输出是类别：共10个类别
- 权重W是784*10的矩阵
- 偏差b是维度为10的行向量
定义softmax操作
- 步骤
  - 1. 对每个项求幂（使用exp）；
  - 1. 对每一行求和（小批量中每个样本是一行），得到每个样本的规范化常数；
  - 1. 将每一行除以其规范化常数，确保结果的和为1。
- $$
  \mathrm{softmax}(\mathbf{X}){ij} = \frac{\exp(\mathbf{X}{ij})}{\sum_k \exp(\mathbf{X}_{ik})}.
  $$

def softmax(X):
   X_exp = torch.exp(X)
   partition = X_exp.sum(1, keepdim=True)
   return X_exp / partition  # 这里应用了广播机制

定义模型

1 2	`def net(X): return softmax(torch.matmul(X.reshape((-1, W.shape[0])), W) + b)`

定义损失函数

1 2	`def cross_entropy(y_hat, y): return - torch.log(y_hat[range(len(y_hat)), y])`

训练
预测

3.7 softmax回归的简洁实现

初始化模型参数

# PyTorch不会隐式地调整输入的形状。因此，
# 我们在线性层前定义了展平层（flatten），来调整网络输入的形状
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10))

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights);

定义损失函数

1	`loss = nn.CrossEntropyLoss(reduction='none')`

定义优化算法

1	`trainer = torch.optim.SGD(net.parameters(), lr=0.1)`

训练

1 2	`num_epochs = 10 d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)`

第四章多层感知机

最简单的深度网络称为_多层感知机_。多层感知机由多层神经元组成，每一层与它的上一层相连，从中接收输入；同时每一层也与它的下一层相连，影响当前层的神经元。

过拟合、欠拟合和模型选择。
权重衰减和暂退法等正则化技术。
数值稳定性和参数初始化相关的问题，

感知机 Proceptron

二分类模型，最早的AI模型之一
收敛定理
求解算法等价于使用批量大小为1的梯度下降。
XOR问题
- 感知机不能拟合XOR函数，它只能产生线性分割面。导致了AI的第一次寒冬。
- 感知机(Perceptron)为什么不能表示异或(XOR) - 腾讯云开发者社区-腾讯云 (tencent.com)
- 多层感知机是如何解决异或问题的？ - 知乎 (zhihu.com)

4.1 多层感知机

视频内容小结：
- 多层感知机使用隐藏层和激活函数来得到非线性模型
- 常用激活函数是Sigmoid，Tanh，ReLU
- 使用softmax来处理多类分类
- 超参数：隐藏层数，各个隐藏层大小
隐藏层
- 线性模型可能会出错
- 我们可以通过在网络中加入一个或多个隐藏层来克服线性模型的限制，使其能处理更普遍的函数关系类型。
- 要做到这一点，最简单的方法是将许多全连接层堆叠在一起。每一层都输出到上面的层，直到生成最后的输出。我们可以把前𝐿−1L−1层看作表示，把最后一层看作线性预测器。这种架构通常称为 _多层感知机_（multilayer perceptron），通常缩写为 _MLP_。
- 输入层不涉及任何计算，因此使用此网络产生输出只需要实现隐藏层和输出层的计算。
非线性
- 为了发挥多层架构的潜力，我们还需要一个额外的关键要素：在仿射变换之后对每个隐藏单元应用非线性的 _激活函数_（activation function）𝜎。激活函数的输出（例如，𝜎(⋅)）被称为 _活性值_（activations）。一般来说，有了激活函数，就不可能再将我们的多层感知机退化成线性模型
激活函数
- _激活函数_（activation function）通过计算加权和并加上偏置来确定神经元是否应该被激活，它们将输入信号转换为输出的可微运算。
- 大多数激活函数都是非线性的。
- _修正线性单元_（Rectified linear unit，_ReLU_）
  - 当输入为负时，ReLU函数的导数为0，而当输入为正时，ReLU函数的导数为1。
  - 注意，当输入值精确等于0时，ReLU函数不可导。
  - 在此时，我们默认使用左侧的导数，即当输入为0时导数为0。
- _参数化ReLU_（Parameterized ReLU，_pReLU_）
- sigmoid函数
  - sigmoid通常称为_挤压函数_（squashing function）
- tanh函数

4.2 多层感知机的从零开始实现

单隐含层，256个隐藏单元

初始化模型参数
设置激活函数
- ReLU
定义模型

定义损失函数

1	`loss = nn.CrossEntropyLoss(reduction='none')`

训练

4.3 多层感知机的简洁实现

定义模型

net = nn.Sequential(nn.Flatten(),
                    nn.Linear(784, 256),
                    nn.ReLU(),
                    nn.Linear(256, 10))

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)
net.apply(init_weights);

4.4 模型选择、欠拟合和过拟合

视频内容小结
- 模型选择
  - 训练误差与泛化误差
  - 训练数据集，验证数据集，测试数据集
    - 训练数据集：训练模型参数
    - 验证数据集：一个用来评估模型好坏的数据集，选择模型超参数
      - 验证数据集不要和训练数据混在一起
    - 测试数据集：只用一次的数据集。
  - k折交叉验证
- 过拟合overfitting、欠拟合underfitting
  - 模型容量
    - 拟合各种函数的能力
    - 低容量的模型难以拟合训练数据
    - 高容量的模型可以记住所有的训练数据
  - 估计模型容量
    - 难以在不同种类的算法之间比较
    - 给定一个模型种类，将有两个主要因素
      - 参数的个数
      - 参数值的选择范围
  - VC维（VC dimension）
    - 统计学习理论的一个核心思想
    - 对于一个分类模型，VC等于一个最大的数据集的大小，不管如何给定标号，都存在一个模型来对它进行完美分类。
    - 计算深度学习模型的VC维很困难
  - 数据复杂度
    - 样本个数
    - 每个样本的元素个数
    - 时间、空间结构
    - 多样性

几个倾向于影响模型泛化的因素：

可调整参数的数量。当可调整参数的数量（有时称为_自由度_）很大时，模型往往更容易过拟合。
参数采用的值。当权重的取值范围较大时，模型可能更容易过拟合。
训练样本的数量。即使你的模型很简单，也很容易过拟合只包含一两个样本的数据集。而过拟合一个有数百万个样本的数据集则需要一个极其灵活的模型。

解决此问题的常见做法是将我们的数据分成三份，除了训练和测试数据集之外，还增加一个 _验证数据集_（validation dataset），也叫 _验证集_（validation set）。但现实是验证数据和测试数据之间的边界模糊得令人担忧。除非另有明确说明，否则在这本书的实验中，我们实际上是在使用应该被正确地称为训练数据和验证数据的数据集，并没有真正的测试数据集。因此，书中每次实验报告的准确度都是验证集准确度，而不是测试集准确度。

4.5 权重衰退（正则化模型的技术）
weight decay

权重衰退等价于L2范数正则化（柔性限制）。
_权重衰减_（weight decay）是最广泛使用的正则化的技术之一，它通常也被称为L2 _正则化_。
将原来的训练目标 _最小化训练标签上的预测损失_，调整为 _最小化预测损失和惩罚项之和_。
正则化常数 λ
小结
- 正则化是处理过拟合的常用方法：在训练集的损失函数中加入惩罚项，以降低学习到的模型的复杂度。
- 保持模型简单的一个特别的选择是使用𝐿2L2惩罚的权重衰减。这会导致学习算法更新步骤中的权重衰减。
- 权重衰减功能在深度学习框架的优化器中提供。
- 在同一训练代码实现中，不同的参数集可以有不同的更新行为。

4.6 暂退法(丢弃法)（Dropout）

动机：一个好的模型需要对输入数据的扰动鲁棒
- 使用有噪音的数据等价于Tikhonov正则
- 丢弃法：在层直接加入噪音（通常将丢弃法作用在隐藏全连接层的输出上）
- 在数据中加入噪音（随机噪音），等价于一个正则
小结
- 丢弃法将一些输出项随机置0来控制模型复杂度；
- 常作用在多层感知机的隐藏层输出上；
- 丢弃概率是控制模型复杂度的超参数。

4.7 前向传播、反向传播、计算图

前向传播 （forward propagation或forward pass）指的是：按顺序（从输入层到输出层）计算和存储神经网络中每层的结果。
反向传播 （backward propagation或backpropagation）指的是计算神经网络参数梯度的方法。简言之，该方法根据微积分中的 链式规则 ，按相反的顺序从输出层到输入层遍历网络。该算法存储了计算某些参数梯度时所需的任何中间变量（偏导数）。（信号前向传播，误差反向传播）
在训练神经网络时，前向传播和反向传播相互依赖。对于前向传播，我们沿着依赖的方向遍历计算图并计算其路径上的所有变量。然后将这些用于反向传播，其中计算顺序与计算图的相反。
因此，在训练神经网络时，在初始化模型参数后，我们交替使用前向传播和反向传播，利用反向传播给出的梯度来更新模型参数 。注意，反向传播重复利用前向传播中存储的中间值，以避免重复计算。带来的影响之一是我们需要保留中间值，直到反向传播完成。这也是训练比单纯的预测需要更多的内存（显存）的原因之一。此外，这些中间值的大小与网络层的数量和批量的大小大致成正比。因此，使用更大的批量来训练更深层次的网络更容易导致 _内存不足_（out of memory）错误。
小结
- 前向传播在神经网络定义的计算图中按顺序计算和存储中间变量，它的顺序是从输入层到输出层。
- 反向传播按相反的顺序（从输出层到输入层）计算和存储神经网络的中间变量和参数的梯度。
- 在训练深度学习模型时，前向传播和反向传播是相互依赖的。
- 训练比预测需要更多的内存。

4.8 数值稳定性和模型初始化

初始化方案的选择在神经网络学习中起着举足轻重的作用，它对保持数值稳定性至关重要。
我们选择哪个函数以及如何初始化参数可以决定优化算法收敛的速度有多快。
糟糕选择可能会导致我们在训练时遇到梯度爆炸或梯度消失。

不稳定梯度带来的风险不止在于数值表示；不稳定梯度也威胁到我们优化算法的稳定性。我们可能面临一些问题。

要么是 梯度爆炸 （gradient exploding）问题：参数更新过大，破坏了模型的稳定收敛；
要么是 梯度消失 （gradient vanishing）问题：参数更新过小，在每次更新时几乎不会移动，导致模型无法学习。
相比于ReLU,sigmoid更容易出现梯度消失。
梯度消失和梯度爆炸是深度网络中常见的问题。在参数初始化时需要非常小心，以确保梯度和参数可以得到很好的控制。
需要用启发式的初始化方法来确保初始梯度既不太大也不太小。
ReLU激活函数缓解了梯度消失问题，这样可以加速收敛。
随机初始化是保证在进行优化前打破对称性的关键。
Xavier初始化表明，对于每一层，输出的方差不受输入数量的影响，任何梯度的方差不受输出数量的影响。
让训练更稳定
- 目标：让梯度值再合理的范围内
  - 将乘法变成加法：ResNet，LSTM
  - 归一化：梯度归一化，梯度剪裁
  - 合理的权重初始化和激活函数

4.9 环境和分布偏移

通过将基于模型的决策引入环境，我们可能会破坏模型。
分布偏移的类型

协变量偏移
标签偏移
概念偏移

第二部分卷积神经网络

第五章深度学习计算

5.1 层和块

一个块可以由许多层组成；一个块可以由许多块组成。
块可以包含代码。
块负责大量的内部处理，包括参数初始化和反向传播。
层和块的顺序连接由Sequential块处理。

5.2 参数管理

我们有几种方法可以访问、初始化和绑定模型参数。
我们可以使用自定义初始化方法。

5.3 延后初始化

延后初始化使框架能够自动推断参数形状，使修改模型架构变得容易，避免了一些常见的错误。
我们可以通过模型传递数据，使框架最终初始化参数。

5.4 自定义层

5.5 读写文件

5.4 GPU

第六章卷积神经网络

_卷积神经网络_（convolutional neural network，CNN）

对于图像数据来说，我们之前在MLP中的操作是，将二维数据变成一个一维向量，但这样的操作忽略了每个图像的空间结构信息。
因为这些网络特征元素的顺序是不变的，因此最优的结果是利用先验知识，即利用相近像素之间的相互关联性，从图像数据中学习得到有效的模型。
本章介绍的_卷积神经网络_（convolutional neural network，CNN）是一类强大的、为处理图像数据而设计的神经网络。
基于卷积神经网络架构的模型在计算机视觉领域中已经占主导地位，当今几乎所有的图像识别、目标检测或语义分割相关的学术竞赛和商业应用都以这种方法为基础。

卷积网络主干的基本元素

卷积层本身、填充（padding）和步幅（stride）的基本细节、用于在相邻区域汇聚信息的汇聚层（pooling）、在每一层中多通道（channel）的使用，以及有关现代卷积网络架构的仔细讨论。
LeNet模型：这是第一个成功应用的卷积神经网络，比现代深度学习兴起时间还要早。

6.1 从全连接层到卷积层
卷积神经网络 （convolutional neural networks，CNN）是机器学习利用自然图像中一些已知结构的创造性方法。

不变性
- 无论哪种方法找到这个物体，都应该和物体的位置无关。
- 卷积神经网络正是将 空间不变性 （spatial invariance）的这一概念系统化，从而基于这个模型使用较少的参数来学习有用的表示。
- 适合于计算机视觉的神经网络架构：
  - 1.平移不变性（translation invariance）：不管检测对象出现在图像中的哪个位置，神经网络的前面几层应该对相同的图像区域具有相似的反应，即为“平移不变性”。
  - 2.局部性（locality）：神经网络的前面几层应该只探索输入图像中的局部区域，而不过度在意图像中相隔较远区域的关系，这就是“局部性”原则。最终，可以聚合这些局部特征，以在整个图像级别进行预测。
小结
- 图像的平移不变性使我们以相同的方式处理局部图像，而不在乎它的位置。
- 局部性意味着计算相应的隐藏表示只需一小部分局部图像像素。
- 在图像处理中，卷积层通常比全连接层需要更少的参数，但依旧获得高效用的模型。
- 卷积神经网络（CNN）是一类特殊的神经网络，它可以包含多个卷积层。
- 多个输入和输出通道使模型在每个空间位置可以获取图像的多方面特征。

6.2 图像卷积

互相关运算

严格来说，卷积层是个错误的叫法，因为它所表达的运算其实是 _互相关运算_（cross-correlation），而不是卷积运算。根据 6.1节中的描述，在卷积层中，输入张量和核张量通过互相关运算产生输出张量。
卷积层
- 卷积层对输入和卷积核权重进行互相关运算，并在添加标量偏置之后产生输出。
- 所以，卷积层中的两个被训练的参数是卷积核权重和标量偏置。
图像中目标的边缘检测
- 简单案例：通过找到像素变化的位置，来检测图像中不同颜色的边缘。
学习卷积核
互相关和卷积
- 为了得到正式的_卷积_运算输出，我们需要执行 (6.1.6)中定义的严格卷积运算，而不是互相关运算。幸运的是，它们差别不大，我们只需水平和垂直翻转二维卷积核张量，然后对输入张量执行 _互相关_运算。
- 为了与深度学习文献中的标准术语保持一致，我们将继续把“互相关运算”称为卷积运算，尽管严格地说，它们略有不同。此外，对于卷积核张量上的权重，我们称其为元素。
特征映射和感受野
- 输出的卷积层有时被称为 特征映射 （feature map），因为它可以被视为一个输入映射到下一层的空间维度的转换器。
- 在卷积神经网络中，对于某一层的任意元素x，其 感受野 （receptive field）是指在前向传播期间可能影响x计算的所有元素（来自所有先前层）。
- 因此，当一个特征图中的任意元素需要检测更广区域的输入特征时，我们可以构建一个更深的网络。
小结
- 二维卷积层的核心计算是二维互相关运算。最简单的形式是，对二维输入数据和卷积核执行互相关操作，然后添加一个偏置。
- 我们可以设计一个卷积核来检测图像的边缘。
- 我们可以从数据中学习卷积核的参数。
- 学习卷积核时，无论用严格卷积运算或互相关运算，卷积层的输出不会受太大影响。
- 当需要检测输入特征中更广区域时，我们可以构建一个更深的卷积网络。

6.3 填充和步幅
填充（padding）和步幅（stride）

在应用了连续的卷积之后，我们最终得到的输出远小于输入大小。这是由于卷积核的宽度和高度通常大于1所导致的。这样会导致原始图像的边界丢失了许多有用信息。而填充是解决此问题最有效的方法。
有时，我们可能希望大幅降低图像的宽度和高度。例如，如果我们发现原始的输入分辨率十分冗余。步幅则可以在这类情况下提供帮助。

填充
- 卷积神经网络中卷积核的高度和宽度通常为奇数，例如1、3、5或7。选择奇数的好处是，保持空间维度的同时，我们可以在顶部和底部填充相同数量的行，在左侧和右侧填充相同数量的列。
- 此外，使用奇数的核大小和填充大小也提供了书写上的便利。对于任何二维张量X，当满足：
  - 1.卷积核的大小是奇数；
  - 2.所有边的填充行数和列数相同；
  - 3.输出与输入具有相同高度和宽度
- 则可以得出：输出Y[i, j]是通过以输入X[i, j]为中心，与卷积核进行互相关计算得到的。
步幅
- 在计算互相关时，卷积窗口从输入张量的左上角开始，向下、向右滑动。在前面的例子中，我们默认每次滑动一个元素。但是，有时候为了高效计算或是缩减采样次数，卷积窗口可以跳过中间位置，每次滑动多个元素。将每次滑动元素的数量称为步幅（stride）
小结
- 填充可以增加输出的高度和宽度。这常用来使输出与输入具有相同的高和宽。
- 步幅可以减小输出的高和宽，例如输出的高和宽仅为输入的高和宽的1/n（n是一个大于1的整数）。
- 填充和步幅可用于有效地调整数据的维度。

6.4 多输入多输出通道
三维张量，对于RGB图像（3 × h × w），把大小为3的这个轴称为通道（channel）维度

多输入通道
- 当输入包含多个通道时，需要构造一个与输入数据具有相同输入通道数的卷积核，以便与输入数据进行互相关运算。
- 多通道输入和多输入通道卷积核之间进行二维互相关运算
  - 于输入和卷积核都有$$c_i$$个通道，我们可以对每个通道输入的二维张量和卷积核的二维张量进行互相关运算，再对通道求和（将$$c_i$$的结果相加）得到二维张量。
多输出通道
- 为了获得多个通道的输出，我们可以为每个输出通道创建一个形状为$$c_i × k_h × k_w$$的卷积核张量，这样卷积核的形状是$$c_o × c_i × k_h × k_w$$。在互相关运算中，每个输出通道先获取所有输入通道，再以对应该输出通道的卷积核计算出结果。
1 × 1 卷积层
- 因为使用了最小窗口，1×1卷积失去了卷积层的特有能力——在高度和宽度维度上，识别相邻元素间相互作用的能力。其实1×1卷积的唯一计算发生在通道上。
小结
- 多输入多输出通道可以用来扩展卷积层的模型。
- 当以每像素为基础应用时，1×1卷积层相当于全连接层。
- 1×1卷积层通常用于调整网络层的通道数量和控制模型复杂性。

6.5 汇聚层
汇聚（pooling）层
它具有双重目的：降低卷积层对位置的敏感性，同时降低对空间降采样表示的敏感性。

最大汇聚层和平均汇聚层

与卷积层类似，汇聚层运算符由一个固定形状的窗口组成，该窗口根据其步幅大小在输入的所有区域上滑动，为固定形状窗口（有时称为 汇聚窗口 ）遍历的每个位置计算一个输出。然而，不同于卷积层中的输入与卷积核之间的互相关计算，汇聚层不包含参数。相反，池运算是确定性的，我们通常计算汇聚窗口中所有元素的最大值或平均值。这些操作分别称为 最大汇聚层 （maximum pooling）和 平均汇聚层 （average pooling）。
填充和步幅
多个通道
- 在处理多通道输入数据时，汇聚层在每个输入通道上单独运算，而不是像卷积层一样在通道上对输入进行汇总。这意味着汇聚层的输出通道数与输入通道数相同。
小结
- 对于给定输入元素，最大汇聚层会输出该窗口内的最大值，平均汇聚层会输出该窗口内的平均值。
- 汇聚层的主要优点之一是减轻卷积层对位置的过度敏感。
- 我们可以指定汇聚层的填充和步幅。
- 使用最大汇聚层以及大于1的步幅，可减少空间维度（如高度和宽度）。
- 汇聚层的输出通道数与输入通道数相同。

6.6 卷积神经网络（LeNet）

AT&T贝尔实验室的研究员Yann LeCun在1989年提出的（并以其命名），目的是识别图像 [LeCun et al., 1998]中的手写数字。

总体来看，LeNet（LeNet-5）由两个部分组成：
- 卷积编码器：由两个卷积层组成;
- 全连接层密集块：由三个全连接层组成。

zh.d2l.ai/_images/lenet.svg
LeNet中的数据流。输入是手写数字，输出为10种可能结果的概率。

小结
- 卷积神经网络（CNN）是一类使用卷积层的网络。
- 在卷积神经网络中，我们组合使用卷积层、非线性激活函数和汇聚层。
- 为了构造高性能的卷积神经网络，我们通常对卷积层进行排列，逐渐降低其表示的空间分辨率，同时增加通道数。
- 在传统的卷积神经网络中，卷积块编码得到的表征在输出之前需由一个或多个全连接层进行处理。
- LeNet是最早发布的卷积神经网络之一。

第七章现代卷积神经网络

虽然深度神经网络的概念非常简单——将神经网络堆叠在一起。但由于不同的网络架构和超参数选择，这些神经网络的性能会发生很大变化。

AlexNet。它是第一个在大规模视觉竞赛中击败传统计算机视觉模型的大型神经网络；
使用重复块的网络（VGG）。它利用许多重复的神经网络块；
网络中的网络（NiN）。它重复使用由卷积层和1×1卷积层（用来代替全连接层）来构建深层网络;
含并行连结的网络（GoogLeNet）。它使用并行连结的网络，通过不同窗口大小的卷积层和最大汇聚层来并行抽取信息；
残差网络（ResNet）。它通过残差块构建跨层的数据通道，是计算机视觉中最流行的体系架构；
稠密连接网络（DenseNet）。它的计算成本很高，但给我们带来了更好的效果。

7.1 深度卷积神经网络（AlexNet）

在上世纪90年代初到2012年之间的大部分时间里，神经网络往往被其他机器学习方法超越，如支持向量机（support vector machines）。

因此，与训练_端到端_（从像素到分类结果）系统不同，经典机器学习的流水线看起来更像下面这样：
1. 获取一个有趣的数据集。在早期，收集这些数据集需要昂贵的传感器（在当时最先进的图像也就100万像素）。
2. 根据光学、几何学、其他知识以及偶然的发现，手工对特征数据集进行预处理。
3. 通过标准的特征提取算法，如SIFT（尺度不变特征变换） [Lowe, 2004]和SURF（加速鲁棒特征） [Bay et al., 2006]或其他手动调整的流水线来输入数据。
4. 将提取的特征送入最喜欢的分类器中（例如线性模型或其它核方法），以训练分类器。

如果你和机器学习研究人员交谈，你会发现他们相信机器学习既重要又美丽：优雅的理论去证明各种模型的性质。机器学习是一个正在蓬勃发展、严谨且非常有用的领域。

如果你和计算机视觉研究人员交谈，你会听到一个完全不同的故事。他们会告诉你图像识别的诡异事实————推动领域进步的是数据特征，而不是学习算法。计算机视觉研究人员相信，从对最终模型精度的影响来说，更大或更干净的数据集、或是稍微改进的特征提取，比任何学习算法带来的进步要大得多。

学习表征
- 另一组研究人员，包括Yann LeCun、Geoff Hinton、Yoshua Bengio、Andrew Ng、Shun ichi Amari和Juergen Schmidhuber，想法则与众不同：他们认为特征本身应该被学习。
- 此外，他们还认为，在合理地复杂性前提下，特征应该由多个共同学习的神经网络层组成，每个层都有可学习的参数。
- 在机器视觉中，最底层可能检测边缘、颜色和纹理。
- 事实上，Alex Krizhevsky、Ilya Sutskever和Geoff Hinton提出了一种新的卷积神经网络变体 _AlexNet_。
- 在网络的最底层，模型学习到了一些类似于传统滤波器的特征抽取器。
- AlexNet的更高层建立在这些底层表示的基础上，以表示更大的特征，如眼睛、鼻子、草叶等等。而更高的层可以检测整个物体，如人、飞机、狗或飞盘。最终的隐藏神经元可以学习图像的综合表示，从而使属于不同类别的数据易于区分。
- 数据
  - ImageNet数据集由斯坦福教授李飞飞小组的研究人员开发，利用谷歌图像搜索（Google Image Search）对每一类图像进行预筛选，并利用亚马逊众包（Amazon Mechanical Turk）来标注每张图片的相关类别。
- 硬件
  - 图形处理器（Graphics Processing Unit，GPU）
  - 当Alex Krizhevsky和Ilya Sutskever实现了可以在GPU硬件上运行的深度卷积神经网络时，一个重大突破出现了。他们意识到卷积神经网络中的计算瓶颈：卷积和矩阵乘法，都是可以在硬件上并行化的操作。于是，他们使用两个显存为3GB的NVIDIA GTX580 GPU实现了快速卷积运算。
AlexNet
- AlexNet使用了8层卷积神经网络 [zh.d2l.ai/_images/alexnet.svg](http://zh.d2l.ai/_images/alexnet.svg)
- AlexNet由八层组成：五个卷积层、两个全连接隐藏层和一个全连接输出层。
- 其次，AlexNet使用ReLU而不是sigmoid作为其激活函数。
- AlexNet通过暂退法（ 4.6节）控制全连接层的模型复杂度，而LeNet只使用了权重衰减。
- AlexNet在训练时增加了大量的图像增强数据，如翻转、裁切和变色。这使得模型更健壮，更大的样本量有效地减少了过拟合。
AlexNet的架构与LeNet相似，但使用了更多的卷积层和更多的参数来拟合大规模的ImageNet数据集。
今天，AlexNet已经被更有效的架构所超越，但它是从浅层网络到深层网络的关键一步。
尽管AlexNet的代码只比LeNet多出几行，但学术界花了很多年才接受深度学习这一概念，并应用其出色的实验结果。这也是由于缺乏有效的计算工具。
Dropout、ReLU和预处理是提升计算机视觉任务性能的其他关键步骤。

7.2 使用块的网络（VGG）
虽然AlexNet证明深层神经网络卓有成效，但它没有提供一个通用的模板来指导后续的研究人员设计新的网络。
使用块的想法首先出现在牛津大学的视觉几何组（visualgeometry group）的_VGG网络_中。通过使用循环和子程序，可以很容易地在任何现代深度学习框架的代码中实现这些重复的架构。

VGG块
经典卷积神经网络的基本组成部分是下面的这个序列：
1. 带填充以保持分辨率的卷积层；
2. 非线性激活函数，如ReLU；
3. 汇聚层，如最大汇聚层。
而一个VGG块与之类似，由一系列卷积层组成，后面再加上用于空间下采样的最大汇聚层。
VGG网络 [zh.d2l.ai/_images/vgg.svg](http://zh.d2l.ai/_images/vgg.svg)

7.3 网络中的网络（NiN）
LeNet、AlexNet和VGG都有一个共同的设计模式：通过一系列的卷积层与汇聚层来提取空间结构特征；然后通过全连接层对特征的表征进行处理。 AlexNet和VGG对LeNet的改进主要在于如何扩大和加深这两个模块。或者，可以想象在这个过程的早期使用全连接层。然而，如果使用了全连接层，可能会完全放弃表征的空间结构。
_网络中的网络_（_NiN_）提供了一个非常简单的解决方案：在每个像素的通道上分别使用多层感知机

NiN的想法是在每个像素位置（针对每个高度和宽度）应用一个全连接层。如果我们将权重连接到每个空间位置，我们可以将其视为1×1卷积层（如 6.4节中所述），或作为在每个像素位置上独立作用的全连接层。从另一个角度看，即将空间维度中的每个像素视为单个样本，将通道维度视为不同特征（feature）。

NiN块以一个普通卷积层开始，后面是两个1×1的卷积层。这两个1×1卷积层充当带有ReLU激活函数的逐像素全连接层。第一层的卷积窗口形状通常由用户设置。随后的卷积窗口形状固定为1×1。

NiN使用由一个卷积层和多个1×1卷积层组成的块。该块可以在卷积神经网络中使用，以允许更多的每像素非线性。
NiN去除了容易造成过拟合的全连接层，将它们替换为全局平均汇聚层（即在所有位置上进行求和）。该汇聚层通道数量为所需的输出数量（例如，Fashion-MNIST的输出为10）。
移除全连接层可减少过拟合，同时显著减少NiN的参数。
NiN的设计影响了许多后续卷积神经网络的设计。

7. 4 含有并行连结的网络（GoogLeNet）

GoogLeNet吸收了NiN中串联网络的思想，并在此基础上做了改进。这篇论文的一个重点是解决了什么样大小的卷积核最合适的问题。

毕竟，以前流行的网络使用小到1×1，大到11×11的卷积核。本文的一个观点是，有时使用不同大小的卷积核组合是有利的。

Inception块
在GoogLeNet中，基本的卷积块被称为 _Inception块_（Inception block）。这很可能得名于电影《盗梦空间》（Inception），因为电影中的一句话“我们需要走得更深”（“We need to go deeper”）。

Inception块由四条并行路径组成。前三条路径使用窗口大小为1×1、3×3和5×5的卷积层，从不同空间大小中提取信息。中间的两条路径在输入上执行1×1卷积，以减少通道数，从而降低模型的复杂性。第四条路径使用3×3最大汇聚层，然后使用1×1卷积层来改变通道数。
这四条路径都使用合适的填充来使输入与输出的高和宽一致，最后我们将每条线路的输出在通道维度上连结，并构成Inception块的输出。在Inception块中，通常调整的超参数是每层输出通道数。

GoogLeNet模型

7.5 批量规范化

训练深层神经网络是十分困难的，特别是在较短的时间内使他们收敛更加棘手。在本节中，我们将介绍 _批量规范化_（batch normalization），这是一种流行且有效的技术，可持续加速深层网络的收敛速度。

为什么需要批量规范化层呢？

首先，数据预处理的方式通常会对最终结果产生巨大影响。
第二，对于典型的多层感知机或卷积神经网络。当我们训练时，中间层中的变量（例如，多层感知机中的仿射变换输出）可能具有更广的变化范围：不论是沿着从输入到输出的层，跨同一层中的单元，或是随着时间的推移，模型参数的随着训练更新变幻莫测。
第三，更深层的网络很复杂，容易过拟合。这意味着正则化变得更加重要。

批量规范化应用于单个可选层（也可以应用到所有层），其原理如下：在每次训练迭代中，我们首先规范化输入，即通过减去其均值并除以其标准差，其中两者均基于当前小批量处理。接下来，我们应用比例系数和比例偏移。正是由于这个基于批量统计的 标准化 ，才有了 批量规范化 的名称。

请注意，如果我们尝试使用大小为1的小批量应用批量规范化，我们将无法学到任何东西。这是因为在减去均值之后，每个隐藏单元将为0。所以，只有使用足够大的小批量，批量规范化这种方法才是有效且稳定的。请注意，在应用批量规范化时，批量大小的选择可能比没有批量规范化时更重要。

由于尚未在理论上明确的原因，优化中的各种噪声源通常会导致更快的训练和较少的过拟合：这种变化似乎是正则化的一种形式。

批量规范化层在”训练模式“（通过小批量统计数据规范化）和“预测模式”（通过数据集统计规范化）中的功能不同。在训练过程中，我们无法得知使用整个数据集来估计平均值和方差，所以只能根据每个小批次的平均值和方差不断训练模型。而在预测模式下，可以根据整个数据集精确计算批量规范化所需的平均值和方差。

批量规范化层
- 全连接层
- 卷积层
- 预测过程中的批量规范化

7.6 残差网络（ResNet）
何恺明等人提出了 _残差网络_（ResNet）

残差网络的核心思想是：每个附加层都应该更容易地包含原始函数作为其元素之一。于是，_残差块_（residual blocks）便诞生了，这个设计对如何建立深层神经网络产生了深远的影响。

一个正常块（左图）和一个残差块（右图）
- ResNet沿用了VGG完整的3×3卷积层设计。
- 残差块里首先有2个有相同输出通道数的3×3卷积层。
- 每个卷积层后接一个批量规范化层和ReLU激活函数。
- 然后我们通过跨层数据通路，跳过这2个卷积运算，将输入直接加在最后的ReLU激活函数前。这样的设计要求2个卷积层的输出与输入形状一样，从而使它们可以相加。
- 如果想改变通道数，就需要引入一个额外的1×1卷积层来将输入变换成需要的形状后再做相加运算。

包含以及不包含 1×1 卷积层的残差块。

ResNet模型

小结
- 学习嵌套函数（nested function）是训练神经网络的理想情况。在深层神经网络中，学习另一层作为恒等映射（identity function）较容易（尽管这是一个极端情况）。
- 残差映射可以更容易地学习同一函数，例如将权重层中的参数近似为零。
- 利用残差块（residual blocks）可以训练出一个有效的深层神经网络：输入可以通过层间的残余连接更快地向前传播。
- 残差网络（ResNet）对随后的深层神经网络设计产生了深远影响。

7.7 稠密神经网络（DenseNet）

_稠密连接网络_（DenseNet）在某种程度上是ResNet的逻辑扩展。

ResNet（左）与 DenseNet（右）在跨层连接上的主要区别：使用相加和使用连结。

稠密网络主要由2部分构成：_稠密块_（dense block）和 过渡层 （transition layer）。前者定义如何连接输入和输出，而后者则控制通道数量，使其不会太复杂。

小结
- 在跨层连接上，不同于ResNet中将输入与输出相加，稠密连接网络（DenseNet）在通道维上连结输入与输出。
- DenseNet的主要构建模块是稠密块和过渡层。
- 在构建DenseNet时，我们需要通过添加过渡层来控制网络的维数，从而再次减少通道的数量。

第三部分计算机视觉

第十二章计算性能

12.1 编译器和解释器
没看

12.2 异步计算
没看

12.3 自动并行
没看

12.4 硬件

CPU
GPU
ASIC

12.5 多GPU训练

在训练和预测时，将一个小批量计算分到多个GPU上来达到加速的目的。
切分方案

数据并行
模型并行
通道并行（数据并行+模型并行）

def allreduce(data):
    for i in range(1, len(data)):
        data[0][:] += data[i].to(data[0].device)
    for i in range(1, len(data)):
        data[i][:] = data[0].to(data[i].device)

12.6 多GPU的简洁实现
没看

12.7 参数服务器
没看

第十三章计算机视觉

13.1 数据增广

图像增广在对训练图像进行一系列的随机变化之后，生成相似但不同的训练样本，从而扩大了训练集的规模。此外，应用图像增广的原因是，随机改变训练样本可以减少模型对某些属性的依赖，从而提高模型的泛化能力。

在线生成图像。

大多数图像增广方法都具有一定的随机性。

翻转和裁剪
改变颜色
多种方法结合

imgaug — imgaug 0.4.0 documentation
一种巧妙且简单的数据增强方法 - MixUp 小综述 - 知乎 (zhihu.com)

目标检测中图像增强，mixup 如何操作？ - 知乎 (zhihu.com)

PyTorch之torchvision.transforms详解[原理+代码实现]_雷恩Layne的博客-CSDN博客_torchvision.transforms

13.2 微调

微调是计算机视觉中，非常重要的技术！！！

应用 迁移学习 （transfer learning）将从_源数据集_学到的知识迁移到_目标数据集_。
尽管ImageNet数据集中的大多数图像与椅子无关，但在此数据集上训练的模型可能会提取更通用的图像特征，这有助于识别边缘、纹理、形状和对象组合。这些类似的特征也可能有效地识别椅子。

迁移学习中的常见技巧: 微调（fine-tuning）。

在源数据集（例如ImageNet数据集）上预训练神经网络模型，即 源模型 。
创建一个新的神经网络模型，即 目标模型 。这将复制源模型上的所有模型设计及其参数（输出层除外）。我们假定这些模型参数包含从源数据集中学到的知识，这些知识也将适用于目标数据集。我们还假设源模型的输出层与源数据集的标签密切相关；因此不在目标模型中使用该层。
向目标模型添加输出层，其输出数是目标数据集中的类别数。然后随机初始化该层的模型参数。
在目标数据集（如椅子数据集）上训练目标模型。输出层将从头开始进行训练，而所有其他层的参数将根据源模型的参数进行微调。

神经网络的网络架构
（一般来说，一个神经网络可以分为两块）

特征抽取讲原始像素变为容易线性分割的特征
线性分类器来做分类

训练

是一个目标数据集上的正常训练任务，但使用更强的正则化。
- 使用更小的学习率
- 使用更少的书籍迭代
源数据集远复杂于目标数据，通常微调效果更好

重用分类器

源数据集可能也有目标数据中的部分标号；
可以使用预训练好的模型分类器中对应标号的向量来做初始化。

固定一些层

神经网络通常学习有层次地特征表示
- 低层的特则更加通用
- 高层次的特则更跟数据集相关
可以固定底部的一些层的参数，不参与更新
- 更强的正则

13.13 实战Kaggle比赛：图像分类（CIFAR-10）

13.14 实战Kagge比赛：狗的品种分类（ImageNet Dogs）

13.3 目标检测和边界框

很多时候图像里有多个我们感兴趣的目标，我们不仅想知道它们的类别，还想得到它们在图像中的具体位置。在计算机视觉里，我们将这类任务称为 目标检测 （object detection）或 目标识别 （object recognition）。

在目标检测中，我们通常使用 边界框（bounding box）来描述对象的空间位置。边界框是矩形的。

两角表示法：由矩形左上角的以及右下角的x和y坐标决定。
中心宽度表示法：边界框中心的(x, y)轴坐标以及框的宽度和高度。

COCO - Common Objects in Context (cocodataset.org)

13.4 锚框
目标检测算法通常会在输入图像中采样大量的区域，然后判断这些区域中是否包含我们感兴趣的目标，并调整区域边界从而更准确地预测目标的 真实边界框 （ground-truth bounding box）。

以每个像素为中心，生成多个缩放比和宽高比（aspect ratio）不同的边界框。这些边界框被称为锚框（anchor box）

如何衡量锚框和真实边界框之间的相似性？ 杰卡德系数 （Jaccard）可以衡量两组之间的相似性。
通过其像素集的杰卡德系数来测量两个边界框的相似性。
对于两个边界框，我们通常将它们的杰卡德系数称为 交并比 （intersection over union，IoU），即两个边界框相交面积与相并面积之比。交并比的取值范围在0和1之间：0表示两个边界框无重合像素，1表示两个边界框完全重合。

为了训练目标检测模型，我们需要每个锚框的_类别_（class）和_偏移量_（offset）标签，其中前者是与锚框相关的对象的类别，后者是真实边界框相对于锚框的偏移量。

小结
- 我们以图像的每个像素为中心生成不同形状的锚框。
- 交并比（IoU）也被称为杰卡德系数，用于衡量两个边界框的相似性。它是相交面积与相并面积的比率。
- 在训练集中，我们需要给每个锚框两种类型的标签。
  - 一个是与锚框中目标检测的类别，
  - 另一个是锚框真实相对于边界框的偏移量（offset）。
- 在预测期间，我们可以使用非极大值抑制（NMS）来移除类似的预测边界框，从而简化输出。

13.6 目标检测数据集

COCO - Common Objects in Context (cocodataset.org)

13. 8 区域卷积神经网络（R-CNN）系列
区域卷积神经网络（region-based CNN或regions with CNN features，R-CNN）]

R-CNN
- 使用启发式搜索算法（Selective search）来选择锚框
- 使用预训练模型来对每个锚框抽取特则
- 训练一个SVM来对类别分类
- 训练一个线性回归模型来预测边缘框偏移

改进方法

快速的R-CNN（Fast R-CNN）
- 使用CNN对图片抽取特征 - 使用RoI池化层对每个锚框生成固定长度的特征
更快的R-CNN（Faster R-CNN）
掩码R-CNN（Mask R-CNN）
小结
R-CNN是最早、也是最有名的一类基于锚框和CNN的目标检测算法。Fast/Faster R-CNN持续提升性能。Faster R-CNN和Mask R-CNN是再要求高精度场景下的常用算法。
- R-CNN对图像选取若干提议区域，使用卷积神经网络对每个提议区域执行前向传播以抽取其特征，然后再用这些特征来预测提议区域的类别和边界框。
- Fast R-CNN对R-CNN的一个主要改进：只对整个图像做卷积神经网络的前向传播。它还引入了兴趣区域汇聚层，从而为具有不同形状的兴趣区域抽取相同形状的特征。
- Faster R-CNN将Fast R-CNN中使用的选择性搜索替换为参与训练的区域提议网络，这样后者可以在减少提议区域数量的情况下仍保证目标检测的精度。
- Mask R-CNN在Faster R-CNN的基础上引入了一个全卷积网络，从而借助目标的像素级位置进一步提升目标检测的精度。

13.7 单发多框检测（SSD：Single Shot Detection）

此模型主要由基础网络组成，其后是几个多尺度特征块。

基本网络用于从输入图像中提取特征，因此它可以使用深度卷积神经网络。

VGG
ResNet

通过多尺度特征块，单发多框检测生成不同大小的锚框，并通过预测边界框的类别和偏移量来检测大小不同的目标，因此这是一个多尺度目标检测模型。

SSD通过单神经网络来检测模型
以每个像素为中心的产生多个锚框
在多个段的输出上进行多尺度的检测
单发多框检测是一种多尺度目标检测模型。基于基础网络块和各个多尺度特征块，单发多框检测生成不同数量和不同大小的锚框，并通过预测这些锚框的类别和偏移量检测不同大小的目标。
在训练单发多框检测模型时，损失函数是根据锚框的类别和偏移量的预测及标注值计算得出的。

13.补充 YOLO（You Only Look Once）

写给小白的YOLO介绍 - 知乎 (zhihu.com)

如何学习yolo？ - 知乎 (zhihu.com)

13. 补充 Center Net

Center Net不是基于锚框的目标检测算法。

基于像素

13.5 多尺度目标检测

因此，当使用较小的锚框检测较小的物体时，我们可以采样更多的区域，而对于较大的物体，我们可以采样较少的区域。

小结
- 在多个尺度下，我们可以生成不同尺寸的锚框来检测不同尺寸的目标。
- 通过定义特征图的形状，我们可以决定任何图像上均匀采样的锚框的中心。
- 我们使用输入图像在某个感受野区域内的信息，来预测输入图像上与该区域位置相近的锚框类别和偏移量。
- 我们可以通过深入学习，在多个层次上的图像分层表示进行多尺度目标检测。

13.9 语义分割和数据集

_语义分割_（semantic segmentation）问题，它重点关注于如何将图像分割成属于不同语义类别的区域。与目标检测不同，语义分割可以识别并理解图像中每一个像素的内容：其语义区域的标注和预测是像素级的。

与目标检测相比，语义分割标注的像素级的边框显然更加精细。

区分：语义分割、图像分割、示例分割

计算机视觉领域还有2个与语义分割相似的重要问题，即 图像分割 （image segmentation）和 实例分割 （instance segmentation）。

图像分割 将图像划分为若干组成区域，这类问题的方法通常利用图像中像素之间的相关性。它在训练时不需要有关图像像素的标签信息，在预测时也无法保证分割出的区域具有我们希望得到的语义。以图13.9.1中的图像作为输入，图像分割可能会将狗分为两个区域：一个覆盖以黑色为主的嘴和眼睛，另一个覆盖以黄色为主的其余部分身体。
实例分割 也叫 同时检测并分割 （simultaneous detection and segmentation），它研究如何识别图像中各个目标实例的像素级区域。与语义分割不同，实例分割不仅需要区分语义，还要区分不同的目标实例。例如，如果图像中有两条狗，则实例分割需要区分像素属于的两条狗中的哪一条。0

数据集：The PASCAL Visual Object Classes Challenge 2012 (VOC2012) (ox.ac.uk)

13.10 转置卷积

_转置卷积_（transposed convolution）用于逆转下采样导致的空间尺寸减小。

转置卷积的填充、步幅和多通道

X = torch.rand(size=(1, 10, 16, 16))

# 卷积
conv = nn.Conv2d(10, 20, kernel_size=5, padding=2, stride=3)
# 转置卷积
tconv = nn.ConvTranspose2d(20, 10, kernel_size=5, padding=2, stride=3)

tconv(conv(X)).shape == X.shape

---
True

小结
- 与通过卷积核减少输入元素的常规卷积相反，转置卷积通过卷积核广播输入元素，从而产生形状大于输入的输出。
- 如果我们将X输入卷积层f来获得输出Y=f(X)并创造一个与f有相同的超参数、但输出通道数是X中通道数的转置卷积层g，那么g(Y)的形状将与X相同。
- 我们可以使用矩阵乘法来实现卷积。转置卷积层能够交换卷积层的正向传播函数和反向传播函数。

13.11 全卷积网络

FCN是用深度神经网络来做语义分割的奠基性工作。
使用转置卷积层来替换CNN最后的全连接层，从而实现每个像素的预测。

_全卷积网络_（fully convolutional network，FCN）采用卷积神经网络实现了从图像像素到像素类别的变换 [Long et al., 2015]。与我们之前在图像分类或目标检测部分介绍的卷积神经网络不同，全卷积网络将中间层特征图的高和宽变换回输入图像的尺寸：这是通过在 13.10节中引入的 转置卷积 （transposed convolution）实现的。因此，输出的类别预测与输入图像在像素级别上具有一一对应关系：通道维的输出即该位置对应像素的类别预测。

13.12 风格迁移

如何使用卷积神经网络，自动将一个图像中的风格应用在另一图像之上，即 风格迁移 （style transfer）

基于卷积神经网络的风格迁移。实线箭头和虚线箭头分别表示前向传播和反向传播

第四部分循环神经网络

第八章循环神经网络

大多数样本并不是独立同分布的（independently and identically distributed，i.i.d.）

简言之，如果说卷积神经网络可以有效地处理空间信息，那么本章的循环神经网络（recurrent neural network，RNN）则可以更好地处理序列信息。 循环神经网络通过引入状态变量存储过去的信息和当前的输入，从而可以确定当前的输出。

8.1 序列模型

时序模型中，当前数据跟之前观察到的数据相关
自回归模型中使用自身过去数据来预测未来
马尔可夫模型假设当前只跟最近少数数据相关，从而简化模型
潜变量模型使用潜变量来概括历史信息

RNN是潜变量模型

8.2 文本预处理

直接看代码！

8.2. 文本预处理 — 动手学深度学习 2.0.0-beta1 documentation (d2l.ai)

8.3 语言模型和数据集

8.4 循环神经网络

对隐状态使用循环计算的神经网络称为循环神经网络（RNN）。
循环神经网络的隐状态可以捕获直到当前时间步序列的历史信息。
循环神经网络模型的参数数量不会随着时间步的增加而增加。
我们可以使用循环神经网络创建字符级语言模型。
我们可以使用困惑度来评价语言模型的质量。

循环神经网络的输出取决于当下输入和前一时间的因变量。
应用到语言模型中时，循环神经网络根据当前词预测下一次时刻词。
使用梯度剪裁解决梯度爆炸的问题

8.5 循环神经网络的从零开始实现

8.5. 循环神经网络的从零开始实现 — 动手学深度学习 2.0.0-beta1 documentation (d2l.ai)

8.6 循环神经网络的简洁实现

8.6. 循环神经网络的简洁实现 — 动手学深度学习 2.0.0-beta1 documentation (d2l.ai)

8.7 通过时间反向传播

“通过时间反向传播”仅仅适用于反向传播在具有隐状态的序列模型。
截断是计算方便性和数值稳定性的需要。截断包括：规则截断和随机截断。
矩阵的高次幂可能导致神经网络特征值的发散或消失，将以梯度爆炸或梯度消失的形式表现。
为了计算的效率，“通过时间反向传播”在计算期间会缓存中间值。

第九章现代循环神经网络

门控循环单元（gated recurrent units，GRU）和 长短期记忆网络（long short-term memory，LSTM）。

9.1 门控循环单元（GRU）

在学术界已经提出了许多方法来解决这类问题。其中最早的方法是”长短期记忆”（long-short-term memory，LSTM） [Hochreiter & Schmidhuber, 1997]，我们将在 9.2节中讨论。门控循环单元（gated recurrent unit，GRU） [Cho et al., 2014a] 是一个稍微简化的变体，通常能够提供同等的效果，并且计算 [Chung et al., 2014]的速度明显更快。由于门控循环单元更简单，我们从它开始解读。

不是每个观察值都是同等重要！

门控隐状态

门控循环单元与普通的循环神经网络之间的关键区别在于：前者支持隐状态的门控。这意味着模型有专门的机制来确定应该何时更新隐状态，以及应该何时重置隐状态。

重置门（reset gate）和更新门（update gate）

重置门允许我们控制“可能还想记住”的过去状态的数量；（能遗忘的机制）
更新门将允许我们控制新状态中有多少个是旧状态的副本。（能关注的机制）

在门控循环单元模型中计算重置门和更新门

候选隐状态（candidate hidden state）

在门控循环单元模型中计算候选隐状态

隐状态

计算门控循环单元模型中的隐状态

门控循环神经网络可以更好地捕获时间步距离很长的序列上的依赖关系。
重置门有助于捕获序列中的短期依赖关系。（遗忘）
更新门有助于捕获序列中的长期依赖关系。（关注）
重置门打开时，门控循环单元包含基本循环神经网络；更新门打开时，门控循环单元可以跳过子序列。

9.2 长短期记忆网络（LSTM）

（long short-term memory，LSTM）

有趣的是，长短期记忆网络的设计比门控循环单元稍微复杂一些，却比门控循环单元早诞生了近20年。

门控记忆元

长短期记忆网络引入了记忆元（memory cell），或简称为单元（cell）。有些文献认为记忆元是隐状态的一种特殊类型，它们与隐状态具有相同的形状，其设计目的是用于记录附加的信息。为了控制记忆元，我们需要许多门。
其中一个门用来从单元中输出条目，我们将其称为输出门（output gate）。
另外一个门用来决定何时将数据读入单元，我们将其称为输入门（input gate）。
我们还需要一种机制来重置单元的内容，由遗忘门（forget gate）来管理，这种设计的动机与门控循环单元相同，能够通过专用机制决定什么时候记忆或忽略隐状态中的输入。

忘记门：将值超0减少
输入门：决定是不是忽略掉输入数据
输出门：决定是不是使用隐状态

候选记忆元

记忆元

隐状态

9.3 深度循环神经网络

事实上，我们可以将多层循环神经网络堆叠在一起，通过对几个简单层的组合，产生了一个灵活的机制。

与多层感知机一样，隐藏层数目L和隐藏单元数目h都是超参数。也就是说，它们可以由我们调整的。另外，用门控循环单元或长短期记忆网络的隐状态来代替 (9.3.1)中的隐状态进行计算，可以很容易地得到深度门控循环神经网络或深度长短期记忆神经网络。

9.4 双向循环神经网络

双向循环神经网络（bidirectional RNNs）添加了反向传递信息的隐藏层

双向循环神经网络的一个关键特性是：使用来自序列两端的信息来估计输出。也就是说，我们使用来自过去和未来的观测信息来预测当前的观测。但是在对下一个词元进行预测的情况中，这样的模型并不是我们所需的。 因为在预测下一个词元时，我们终究无法知道下一个词元的下文是什么，所以将不会得到很好的精度。具体地说，在训练期间，我们能够利用过去和未来的数据来估计现在空缺的词；而在测试期间，我们只有过去的数据，因此精度将会很差。下面的实验将说明这一点。

另一个严重问题是，双向循环神经网络的计算速度非常慢。其主要原因是网络的前向传播需要在双向层中进行前向和后向递归，并且网络的反向传播还依赖于前向传播的结果。因此，梯度求解将有一个非常长的链。

在双向循环神经网络中，每个时间步的隐状态由当前时间步的前后数据同时决定。
双向循环神经网络与概率图模型中的“前向-后向”算法具有相似性。
双向循环神经网络主要用于序列编码和给定双向上下文的观测估计。
由于梯度链更长，因此双向循环神经网络的训练代价非常高。
通常应用在对序列的特征提取、填空，不会用在预测未来。

lstm_layer = nn.LSTM(num_inputs, num_hiddens, num_layers, bidirectional=True)
model = d2l.RNNModel(lstm_layer, len(vocab))

# bidirectional=True

9.5 机器翻译与数据集

语言模型是自然语言处理的关键，而机器翻译是语言模型最成功的基准测试。因为机器翻译正是将输入序列转换成输出序列的 序列转换模型（sequence transduction）的核心问题。

机器翻译（machine translation）指的是将序列从一种语言自动翻译成另一种语言。

因为统计机器翻译（statisticalmachine translation）涉及了翻译模型和语言模型等组成部分的统计分析，因此基于神经网络的方法通常被称为 神经机器翻译（neuralmachine translation），用于将两种翻译模型区分开来。

9.6 编码器-解码器架构

编码器（Encoder）：讲文本表示成向量
解码器（Decoder）：将向量表示成输出

一个模型被分为两块

编码器处理输出
解码器生成输出

9.7 序列到序列学习（seq2seq）

seq2seq从一个句子生成另一个句子
编码器和解码器都是RNN
将编码器最后时间隐状态来初始化解码器隐状态来完成信息传递
常用BLEU来衡量生成序列的好坏

9.8 束搜索

贪心搜索（greedy search）策略

效率最高，但不一定是最好的。

穷举搜索（exhaustive search）

保证是最好的，但是计算复杂度太高了。

束搜索（beam search）

束搜索（beam search）是贪心搜索的一个改进版本。它有一个超参数，名为束宽（beam size）k。在时间步1，我们选择具有最高条件概率的k个词元。这k个词元将分别是k个候选输出序列的第一个词元。在随后的每个时间步，基于上一时间步的k个候选输出序列，我们将继续从k|Y|个可能的选择中挑出具有最高条件概率的k个候选输出序列。

实际上，贪心搜索可以看作是一种束宽为1的特殊类型的束搜索。通过灵活地选择束宽，束搜索可以在正确率和计算代价之间进行权衡。

第五部分注意力机制

第十章注意力机制

10.1 注意力提示

双组件（two-component）: 在这个框架中，受试者基于非自主性提示和自主性提示 有选择地引导注意力的焦点。

由于突出性的非自主性提示（红杯子），注意力不自主地指向了咖啡杯
依赖于任务的意志提示（想读一本书），注意力被自主引导到书上

因此，“是否包含自主性提示”将注意力机制与全连接层或汇聚层区别开来。

在注意力机制的背景下，我们将自主性提示称为查询（query）。

给定任何查询，注意力机制通过注意力汇聚（attention pooling）将选择引导至感官输入（sensory inputs，例如中间特征表示）。

在注意力机制中，这些感官输入被称为值（value）。更通俗的解释，每个值都与一个键（key）配对，这可以想象为感官输入的非自主提示。

query(Volitional cue 自主性提示)
key（Non-volitional cue 非自主性提示）
value（sensory inputs）
attention pooling

如图10.1.3所示，我们可以设计注意力汇聚，以便给定的查询（自主性提示）可以与键（非自主性提示）进行匹配，这将引导得出最匹配的值（感官输入）。

注意力机制通过注意力汇聚将*查询*（自主性提示）和*键*（非自主性提示）结合在一起，实现对*值*（感官输入）的选择倾向

10.2 注意力汇聚：Nadaraya-Watson核回归

Query查询（自主提示）和Key键（非自主提示）之间的交互形成了注意力汇聚（Attention pooling），注意力汇聚有选择地聚合了Value值（感官输入）以生成最终的输出。

10.3 注意力评分函数

注意力分数是query和key的相似度，注意力权重是分数的softmax结果
常见的分数计算
- 将query和key合并起来进入一个单输出单隐藏层的MLP:加性注意力（additive attention）
- 直接将query和key做内积:缩放点积注意力（scaled dot-product attention）

10.4 Bahdanau 注意力

使用注意力机制的seq2seq

10.5 多头注意力

在实践中，当给定相同的查询、键和值的集合时，我们希望模型可以基于相同的注意力机制学习到不同的行为，然后将不同的行为作为知识组合起来，捕获序列内各种范围的依赖关系（例如，短距离依赖和长距离依赖关系）。因此，允许注意力机制组合使用查询、键和值的不同 子空间表示（representation subspaces）可能是有益的。

与其只使用单独一个注意力汇聚，我们可以用独立学习得到的组不同的 线性投影（linear projections）来变换查询、键和值。然后，这组变换后的查询、键和值将并行地送到注意力汇聚中。最后，将这个注意力汇聚的输出拼接在一起，并且通过另一个可以学习的线性投影进行变换，以产生最终输出。这种设计被称为多头注意力（multihead attention） [Vaswani et al., 2017]。对于个注意力汇聚输出，每一个注意力汇聚都被称作一个头（head）。

多头注意力：多个头连结然后线性变换

10.6 自注意力和位置编码

有了注意力机制之后，我们将词元序列输入注意力汇聚（attention pooling）中，以便同一组词元同时充当查询、键和值。具体来说，每个查询都会关注所有的键－值对并生成一个注意力输出。 *由于查询、键和值来自同一组输入，因此被称为 自注意力（self-attention）* [Lin et al., 2017b, Vaswani et al., 2017]，也被称为内部注意力（intra-attention） [Cheng et al., 2016, Parikh et al., 2016, Paulus et al., 2017]。

自注意力同时具有并行计算和最短的最大路径长度这两个优势。

在处理词元序列时，循环神经网络是逐个的重复地处理词元的，而自注意力则因为并行计算而放弃了顺序操作。为了使用序列的顺序信息，我们通过在输入表示中添加 位置编码（positional encoding）来注入绝对的或相对的位置信息。位置编码可以通过学习得到也可以直接固定得到。

10.7 Transformer

对比之前仍然依赖循环神经网络实现输入表示的自注意力模型 [Cheng et al., 2016, Lin et al., 2017b, Paulus et al., 2017]，transformer模型完全基于注意力机制，没有任何卷积层或循环神经网络层 [Vaswani et al., 2017]。

transformer是由编码器和解码器组成的。

transformer的编码器和解码器是基于自注意力的模块叠加而成的，源（输入）序列和目标（输出）序列的嵌入（embedding）表示将加上位置编码（positional encoding），再分别输入到编码器和解码器中。

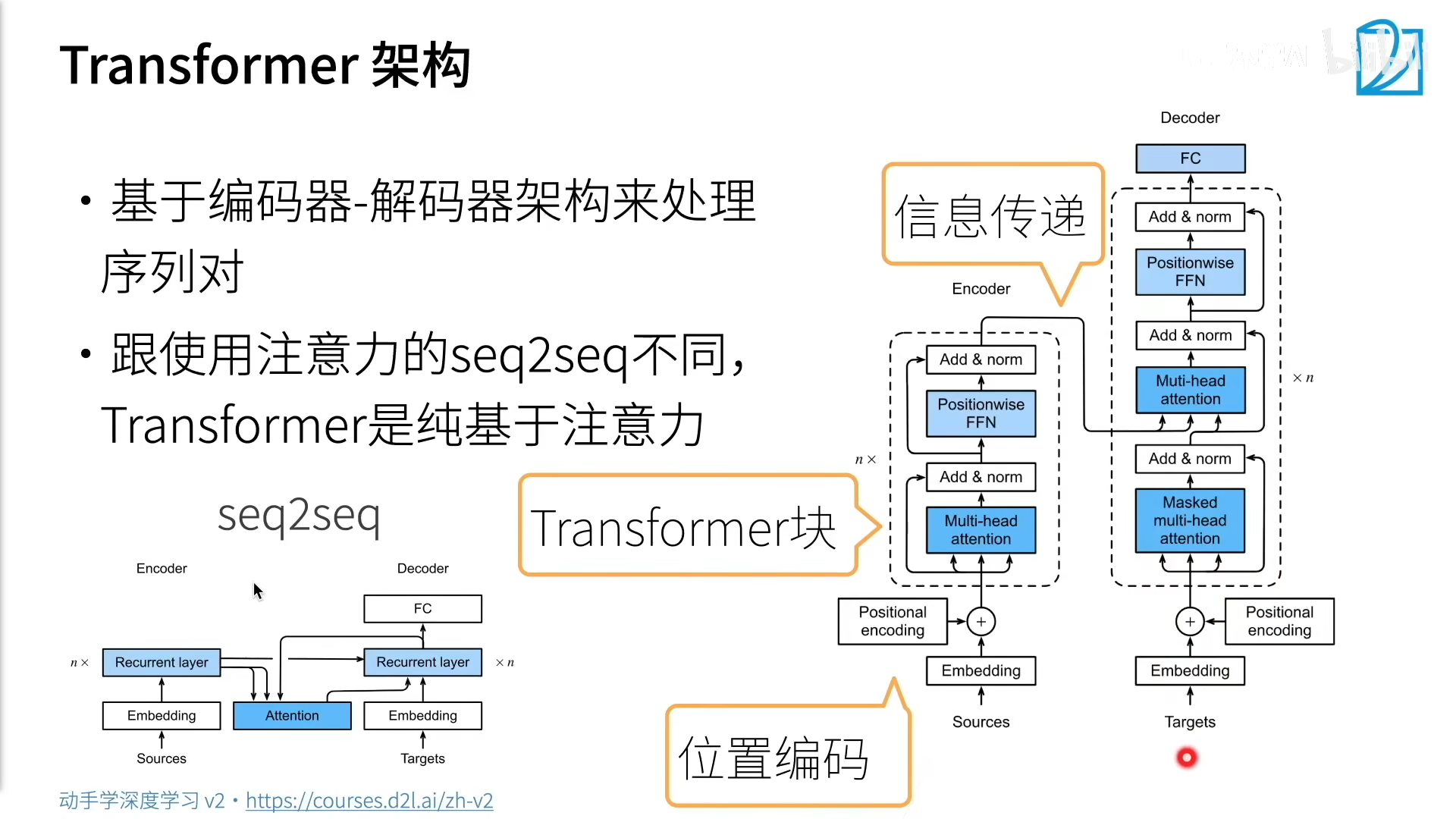
编码器部分：

从宏观角度来看，transformer的编码器是由多个相同的层叠加而成的，每个层都有两个子层（子层表示为）。

第一个子层是多头自注意力（multi-head self-attention）汇聚；
第二个子层是基于位置的前馈网络（positionwise feed-forward network）。

在计算编码器的自注意力时，查询、键和值都来自前一个编码器层的输出。

每个子层都采用了残差连接（residual connection）。

层规范化（layer normalization）

解码器部分：

Transformer解码器也是由多个相同的层叠加而成的，并且层中使用了残差连接和层规范化。

除了编码器中描述的两个子层之外，解码器还在这两个子层之间插入了第三个子层，称为编码器－解码器注意力（encoder-decoder attention）层。

在编码器－解码器注意力中，查询来自前一个解码器层的输出，而键和值来自整个编码器的输出。

在解码器自注意力中，查询、键和值都来自上一个解码器层的输出。但是，解码器中的每个位置只能考虑该位置之前的所有位置。这种掩蔽（masked）注意力保留了自回归（auto-regressive）属性，确保预测仅依赖于已生成的输出词元。

第十四章自然语言处理：预训练

14.1. 词嵌入（Word2vec）

14.2. 近似训练

14.3. 用于预训练词嵌入的数据集

14.4. 预训练word2vec

14.5. 全局向量的词嵌入（GloVe）

14.6. 子词嵌入

14.7. 词的相似性和类比任务

14.8. 来自Transformers的双向编码器表示（BERT）

掩蔽语言模型（Masked Language Modeling）

如 8.3节所示，语言模型使用左侧的上下文预测词元。为了双向编码上下文以表示每个词元，BERT随机掩蔽词元并使用来自双向上下文的词元以自监督的方式预测掩蔽词元。此任务称为掩蔽语言模型。

在这个预训练任务中，将随机选择15%的词元作为预测的掩蔽词元。要预测一个掩蔽词元而不使用标签作弊，一个简单的方法是总是用一个特殊的“”替换输入序列中的词元。然而，人造特殊词元“”不会出现在微调中。为了避免预训练和微调之间的这种不匹配，如果为预测而屏蔽词元（例如，在“this movie is great”中选择掩蔽和预测“great”），则在输入中将其替换为：

80%时间为特殊的““词元（例如，“this movie is great”变为“this movie is”；
10%时间为随机词元（例如，“this movie is great”变为“this movie is drink”）；
10%时间内为不变的标签词元（例如，“this movie is great”变为“this movie is great”）。

请注意，在15%的时间中，有10%的时间插入了随机词元。这种偶然的噪声鼓励BERT在其双向上下文编码中不那么偏向于掩蔽词元（尤其是当标签词元保持不变时）。

下一句预测（Next Sentence Prediction）

尽管掩蔽语言建模能够编码双向上下文来表示单词，但它不能显式地建模文本对之间的逻辑关系。为了帮助理解两个文本序列之间的关系，BERT在预训练中考虑了一个二元分类任务——下一句预测。在为预训练生成句子对时，有一半的时间它们确实是标签为“真”的连续句子；在另一半的时间里，第二个句子是从语料库中随机抽取的，标记为“假”。

14.9. 用于预训练BERT的数据集

14.10. 预训练BERT

原始BERT [Devlin et al., 2018]有两个不同模型尺寸的版本。基本模型（）使用12层（Transformer编码器块），768个隐藏单元（隐藏大小）和12个自注意头。大模型（）使用24层，1024个隐藏单元和16个自注意头。值得注意的是，前者有1.1亿个参数，后者有3.4亿个参数。为了便于演示，我们定义了一个小的BERT，使用了2层、128个隐藏单元和2个自注意头。

第十五章自然语言处理：应用

15.1. 情感分析及数据集（Word2vec）

15.2. 情感分析：使用循环神经网络

15.3. 情感分析：使用卷积神经网络

15.4. 自然语言推断与数据集

15.5. 自然语言推断：使用注意力

15.6. 针对序列级和词元级应用程序微调BERT

15.7. 自然语言推断：微调BERT

第十一章优化算法

优化
- 全局最优，局部最优
凸优化
- 凸：线性回归，Softmax回归
- 非凸：其他（MLP, CNN, RNN, Attention……）
优化算法
- 梯度下降（gradient descent）
- 随机梯度下降（stochastic gradient descent，SGD）
- 小批量随机梯度下降（Mini-Batch Gradient Descent）
- Adam算法：对学习率不敏感